
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln4 |
| 4 |
| lnn |
| n |
| 1 |
| n |
| lnn |
| n |
| n-1 |
| n |
| a(1-x) |
| x |
| lnn |
| n |
| n-1 |
| n |
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln4 |
| 4 |
| lnn |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n-1 |
| n |
| 1 |
| n |


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
| 2011 | ||
|
| 2011 | ||
|
| 2013 | ||
|
| 2013 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| DA |
| DB |
| DC |
| 0 |
| EC |
| 3 |
| EA |
| 3 |
| EB |
| DE |
| AB |
| OM |
| ON |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
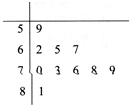 已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.
已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com