
| 本数 人数 性别 | 0 | 1 | 2 | 3 | 4 | 5 |
| 男生 | 0 | 1 | 4 | 3 | 2 | 2 |
| 女生 | 0 | 0 | 1 | 3 | 3 | 1 |
分析 (Ⅰ)利用公式分别求出男生、女生阅读名著本数的平均数与方差即可;(Ⅱ)利用列举法计算基本事件数,即可求出对应的概率值.
解答 解:(Ⅰ)全班有12个男生8个女生,
∴男生阅读名著本数的平均值x1=$\frac{1×1+4×2+3×3+2×4+2×5}{12}$=3,
女生阅读名著本数的平均值x2=$\frac{1×2+3×3+3×4+1×5}{8}$=3.5,
∴$s_1^2=\frac{{1×{{({1-3})}^2}+4×{{({2-3})}^2}+3×{{({3-3})}^2}+2×{{({4-3})}^2}+2×{{({5-3})}^2}}}{12}=1.5$,
$s_2^2=\frac{{1×{{({2-\frac{7}{2}})}^2}+3×{{({3-\frac{7}{2}})}^2}+3×{{({4-\frac{7}{2}})}^2}+1×{{({5-\frac{7}{2}})}^2}}}{8}=3$;
(II)阅读4本名著的学生共有5人,其中两名男生,三名女生,
设两名男生分别为 A1,A2,三名女生分别为 B1,B2,B3,
从这5人中任选两人的选法有:
A1 A2,A1 B1,A1 B2,A1 B3,A2 B1,
A2 B2,A2 B3,B1 B2,B1 B3,B2 B3共10种,
其中一男一女的选法有:
A1 B1,A1 B2,A1 B3,A2 B1,A2 B2,A2 B3共6种,
所以从这5人中选出的两人是一男一女的概率为$\frac{6}{10}=0.6$.
点评 本题考查了平均数与方差的计算问题,也考查了用列举法求古典概型的概率问题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 1007 | C. | 2016 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 本数 人数 性别 | 0 | 1 | 2 | 3 | 4 | 5 |
| 男生 | 0 | 1 | 4 | 3 | 2 | 2 |
| 女生 | 0 | 0 | 1 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M+m=4 | B. | M+m=3 | C. | M-m=4 | D. | M-m=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
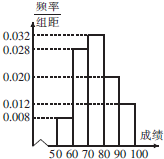 博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次APEC知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.
博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次APEC知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | $\frac{16}{3}$π | C. | 6π | D. | $\frac{20}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com