
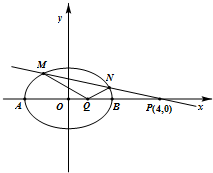
 已知椭圆C的左右顶点分别为A(-2,0),B(2,0),椭圆上除A、B外的任一点C满足kAC•kBC=-$\frac{1}{2}$.
已知椭圆C的左右顶点分别为A(-2,0),B(2,0),椭圆上除A、B外的任一点C满足kAC•kBC=-$\frac{1}{2}$.分析 (1)由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),设椭圆上的任意一点C(x,y),由kAC•kBC=-$\frac{1}{2}$,利用斜率计算公式可得$\frac{y}{x+2}•\frac{y}{x-2}$=-$\frac{1}{2}$,整理化简即可得出.
(2)假设在x轴上存在点Q,使得∠PQM+∠PQN=180°,设直线QM,QN的斜率存在,分别设为k1,k2,等价于k1+k2=0.设直线l的方程为y=k(x-4),与椭圆方程联立化为:(2k2+1)x2-16k2x+32k2-4=0,设M(x1,y1),N(x2,y2),设Q(m,0),则k1+k2=$\frac{{y}_{1}}{{x}_{1}-m}$+$\frac{{y}_{2}}{{x}_{2}-m}$=0.化为:k(x1-4)(x2-m)+k(x2-4)(x1-m)=0,把根与系数的关系代入即可得出.
解答 解:(1)由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
设椭圆上的任意一点C(x,y),∵kAC•kBC=-$\frac{1}{2}$,
∴$\frac{y}{x+2}•\frac{y}{x-2}$=-$\frac{1}{2}$,整理化为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1.
点A(-2,0),B(2,0),也满足上述方程,
∴椭圆C的标准方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1.
(2)假设在x轴上存在点Q,使得∠PQM+∠PQN=180°,
设直线QM,QN的斜率存在,分别设为k1,k2,等价于k1+k2=0.
设直线l的方程为y=k(x-4),联立$\left\{\begin{array}{l}{y=k(x-4)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,化为:(2k2+1)x2-16k2x+32k2-4=0,
则△=256k4-4(2k2+1)(32k2-4)>0,化为k2$<\frac{1}{6}$.
设M(x1,y1),N(x2,y2),则x1+x2=$\frac{16{k}^{2}}{2{k}^{2}+1}$,x1•x2=$\frac{32{k}^{2}-4}{2{k}^{2}+1}$,
设Q(m,0),则k1+k2=$\frac{{y}_{1}}{{x}_{1}-m}$+$\frac{{y}_{2}}{{x}_{2}-m}$=0.又y1=k(x1-4),y2=k(x2-4),
化为:k(x1-4)(x2-m)+k(x2-4)(x1-m)=0,
∴k=0,或2x1x2-(m+4)(x1+x2)+8m=0,
∴2×$\frac{32{k}^{2}-4}{2{k}^{2}+1}$-(m+4)×$\frac{16{k}^{2}}{2{k}^{2}+1}$+8m=0,化为:m-1=0,解得m=1.
k=0时也成立.
综上可得:在x轴上存在点Q(1,0),使得∠PQM+∠PQN=180°.
点评 本题考查了椭圆的标准方程、斜率计算公式、直线与椭圆相交转化为一元二次方程的根与系数的关系、恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
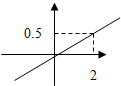 某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A,B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图所示,B品牌的销售利润y2与投入资金x的关系为y2=$\frac{3}{4}\sqrt{x}$.
某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A,B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图所示,B品牌的销售利润y2与投入资金x的关系为y2=$\frac{3}{4}\sqrt{x}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com