
分析 (1)将函数y=f(x+1)的图象向右平移一个单位得到函数y=f(x)的图象,得出函数y=f(x)的图象关于点(0,0)对称,即y=f(x)为奇函数,所以f(x)=a1x3+a3x.利用当x=-1时,f(x)取得极大值$\frac{2}{3}$,列出方程组,求解a1,a3.即可求函数f(x)的表达式;
(2)先证明ln(1+x)<x成立,即可证明结论;
(3)确定当n≥4时,有$\frac{({b}_{n+1})^{(n+1)(n+2)}}{{(b}_{n})^{(n+1)(n+2)}}$<1,所以当n≥4时,bn>bn+1,即:b4>b5>b6>…,即可得出结论.
解答 (1)解:将函数y=f(x+1)的图象向右平移一个单位,得到函数y=f(x)的图象,
∴函数y=f(x)的图象关于点(0,0)对称,即函数y=f(x)是奇函数,
∴f(x)=a1x3+a3x
∴f′(x)=3a1x2+a3
由题意得:3a1+a3=0且-3a1-a3=$\frac{2}{3}$,
∴a1=$\frac{1}{3}$,a3=-1,
∴f(x)=$\frac{1}{3}$x3-x,经检验满足题意;
(2)证明:由(1)可知g(x)=x,
∴x>0时,[1+$\frac{1}{g(x)}$]g(x)<e,可化为ln(1+$\frac{1}{x}$)<$\frac{1}{x}$.
构造函数h(x)=ln(1+x)-x(x>0).则h′(x)=-$\frac{x}{1+x}$<0,
∴函数h(x)在(0,+∞)上是减函数,
∴h(x)<h(0)=0,
∴x>0时,ln(1+x)<x,
∴ln(1+$\frac{1}{x}$)<$\frac{1}{x}$,
∴x>0时,[1+$\frac{1}{g(x)}$]g(x)<e;
(3)解:bn=g(n)${\;}^{\frac{1}{g(n+1)}}$=${n}^{\frac{1}{n+1}}$
所以$\frac{({b}_{n+1})^{(n+1)(n+2)}}{{(b}_{n})^{(n+1)(n+2)}}$=$\frac{n+1}{{n}^{2}}$•($1+\frac{1}{n})^{n}$<$\frac{3(n+1)}{{n}^{2}}$,
令$\frac{3(n+1)}{{n}^{2}}$<1,得:n2-3n-3>0,结合n∈N*得:n≥4,
因此,当n≥4时,有$\frac{({b}_{n+1})^{(n+1)(n+2)}}{{(b}_{n})^{(n+1)(n+2)}}$<1,
所以当n≥4时,bn>bn+1,即:b4>b5>b6>…,
又通过比较b1、b2、b3、b4的大小知:b1<b2<b3<b4,
因为b1=1,且n≠1时bn≠1,所以若数列{bn}中存在相等的两项,只能是b2、b3与后面的项可能相等,
又b2=b8,b3=${3}^{\frac{1}{4}}$>b5=${5}^{\frac{1}{6}}$,所以数列{bn}中存在唯一相等的两项,
即:b2=b8.
点评 本题考查了数列与函数的综合应用,考查了利用导数研究函数的单调性和最值问题,也考查了数列与不等式的应用,是较难的题目.


科目:高中数学 来源: 题型:选择题
| A. | 有两边及一边的对角对应相等的两个三角形全等 | |
| B. | 两边相等的两直角三角形全等 | |
| C. | 有两个角及第三个角的对边对应相等的两个三角形全等 | |
| D. | 有两个角及一边相等的两个三角形全等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
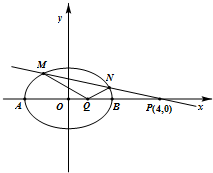 已知椭圆C的左右顶点分别为A(-2,0),B(2,0),椭圆上除A、B外的任一点C满足kAC•kBC=-$\frac{1}{2}$.
已知椭圆C的左右顶点分别为A(-2,0),B(2,0),椭圆上除A、B外的任一点C满足kAC•kBC=-$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com