
 如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,
如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,分析 (1)求出,∠ABD=60°,∠BAD=180°-60°-75°=45°,利用正弦定理,求BD的长;
(2)利用△ABD的面积+△BCD的面积-△ACD的面积,即可求△ABC的面积.
解答 解:(1)在△ABD中,AD=$\sqrt{6}$,∠ABD=60°,∠BAD=180°-60°-75°=45°,
由正弦定理得 $\frac{BD}{sin45°}$=$\frac{\sqrt{6}}{sin60°}$,所以BD=2.…(4分)
(2)在△ABD中,AD=$\sqrt{6}$,BD=2,∠ADB=75°,
所以△ABD的面积S1=$\frac{1}{2}$AD•BD•sin∠ADB=$\frac{3+\sqrt{3}}{2}$.…(8分)
又△ACD的面积S2=$\frac{1}{2}$AD•DC•sin∠ADC=$\frac{3}{2}$,…(10分)
△BCD的面积S3=1.…(12分)
所以△ABC的面积S=S1+S3-S2=$\frac{2+\sqrt{3}}{2}$.…(14分)
点评 本题考查正弦定理,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | AD•AB=CD2 | B. | CE•CB=AD•AB | C. | CE•CB=AD•DB | D. | CE•EB=CD2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{x-q}^{x-19}$ | B. | A${\;}_{x-q}^{x-20}$ | C. | A${\;}_{x-q}^{19-q}$ | D. | A${\;}_{x-q}^{20-q}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
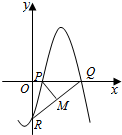 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )| A. | 2$\sqrt{3}$ | B. | $\frac{7\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com