
分析 根据倾斜角与斜率的关系,可判断①;根据三角函数在各个象限的符号,可判断②;根据点斜式方程的适用范围,可判断③;根据象限角的定义,可判断④;根据两圆位置关系,可判断⑤.
解答 解:①一条直线的倾斜角为α,则它的斜率为k=tanα,当α=90°时,直线的斜率不存在,故错误;
②若tanθ•cosθ=sinθ>0,且cosθ≠0,则θ在第一二象限,故正确;
③方程y=k(x-2)表示通过(2,0)的且斜率存在的直线,故错误;
④锐角是第一象限角,但第一象限角不都是锐角,故错误;
⑤若两圆x2+(y+1)2=1和(x+1)2+y2=r2相交,则|r-1|<$\sqrt{2}$<r+1,则实数r的取值范围区间是($\sqrt{2}$-1,$\sqrt{2}+1$),故错误;
即正确的命题的序号是②,
故答案为:②
点评 本题以命题的真假判断为载体,考查了倾斜角,三角函数的符号,点斜式方程,象限角,两圆位置关系等知识点,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
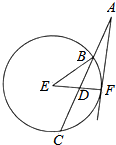 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | k-1 | C. | k | D. | 2k |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,
如图,在平面四边形ABCD中,AD=$\sqrt{6}$,CD=$\sqrt{2}$,∠ABD=60°,∠ADB=75°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com