
| A. | 3f(3ln2)>2f(3ln3) | B. | 3f(3ln2)与2f(3ln3)的大小不确定 | ||
| C. | 3f(3ln2)=2f(3ln3) | D. | 3f(3ln2)<2f(3ln3) |
分析 根据选项可构造函数h(x)=$\frac{f(3lnx)}{x}$,利用导数判断函数h(x)的单调性,进而可比较h(2)与h(3)的大小,从而得到答案.
解答 解:令h(x)=$\frac{f(3lnx)}{x}$,则h′(x)=$\frac{3f′(3lnx)-f(3lnx)}{{x}^{2}}$,
因为对任意的x∈R都有3f′(x)>f(x)成立,所以3f′(3lnx)>f(3lnx),
所以h′(x)>0,h(x)在(0,+∞)上单调递增,
所以h(2)<h(3),即$\frac{f(3ln2)}{2}$<$\frac{f(3ln3)}{3}$,
所以3f(3ln2)<2f(3ln3).
故选D.
点评 本题考查了导数的运算法则,利用导数判断函数的单调性.合理构造函数是解决问题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
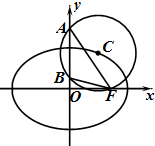 已知点C(x0,y0)是椭圆$\frac{{x}^{2}}{2}$+y2=1上的动点,以C为圆心的圆过点F(1,0).
已知点C(x0,y0)是椭圆$\frac{{x}^{2}}{2}$+y2=1上的动点,以C为圆心的圆过点F(1,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R+,e${\;}^{{x}_{0}}$<lnx0 | B. | ?x∈R+,e^x<lnx | ||
| C. | ?x0∈R+,e${\;}^{{x}_{0}}$≤lnx0 | D. | ?x∈R+,e^x≤lnx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com