
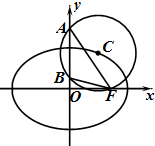
 已知点C(x0,y0)是椭圆$\frac{{x}^{2}}{2}$+y2=1上的动点,以C为圆心的圆过点F(1,0).
已知点C(x0,y0)是椭圆$\frac{{x}^{2}}{2}$+y2=1上的动点,以C为圆心的圆过点F(1,0).分析 (Ⅰ)当圆C与y轴相切时,|x0|=$\sqrt{({x}_{0}-1)^{2}+{{y}_{0}}^{2}}$,再由点C在椭圆上,得$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}=1$,由此能求出实数x0的值.
(Ⅱ)圆C的方程是(x-x0)2+(y-y0)2=(x0-1)2+${{y}_{0}}^{2}$,令x=0,得y2-2y0y+2x0-1=0,由此利用根的判别式、韦达定理,结合已知条件能求出|FA|•|FB|的取值范围.
解答 解:(Ⅰ)当圆C与y轴相切时,|x0|=$\sqrt{({x}_{0}-1)^{2}+{{y}_{0}}^{2}}$,(2分)
又因为点C在椭圆上,所以$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}=1$,(3分)
解得${x}_{0}=-2±2\sqrt{2}$,(5分)
因为-$\sqrt{2}≤{x}_{0}≤\sqrt{2}$,所以${x}_{0}=-2+2\sqrt{2}$.(6分)
(Ⅱ)圆C的方程是(x-x0)2+(y-y0)2=(x0-1)2+${{y}_{0}}^{2}$,
令x=0,得y2-2y0y+2x0-1=0,
设A(0,y1),B(0,y2),则y1+y2=2y0,y1y2=2x0-1,(8分)
由$△=4{{y}_{0}}^{2}-4(2{x}_{0}-1)>0$,及${{y}_{0}}^{2}=1-\frac{1}{2}{{x}_{0}}^{2}$得-2-2$\sqrt{2}$<x0<-2+2$\sqrt{2}$,
又由P点在椭圆上,-$\sqrt{2}$≤x0≤$\sqrt{2}$,所以-$\sqrt{2}$≤${x}_{0}<-2+2\sqrt{2}$,(10分)
|FA|•|FB|=$\sqrt{{{y}_{1}}^{2}+1}$•$\sqrt{{{y}_{2}}^{2}+1}$=$\sqrt{({y}_{1}{y}_{2})^{2}+({{y}_{1}}^{2}+{{y}_{2}}^{2})+1}$(12分)
=$\sqrt{(2{x}_{0}-1)^{2}+4{y}_{0}{\;}^{2}-2(2{x}_{0}-1)+1}$
=$\sqrt{2{{x}_{0}}^{2}-8{x}_{0}+8}$
=$\sqrt{2}(2-{x}_{0})$,(14分)
所以|FA|•|FB|的取值范围是(4$\sqrt{2}-4$,2$\sqrt{2}$+2].(15分)
点评 本题考查实数值的求法,考查两线段乘积的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、圆、椭圆性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要的条件 | B. | 必要而不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要的条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆心角为1弧度的扇形的弧长都相等 | |
| B. | 角α是第四象限角,则2kπ-$\frac{π}{2}$<α<2kπ(k∈Z) | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 第一象限的角是锐角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [e2,3e] | B. | (e2,3e) | C. | (7,3e] | D. | (e2,7)∪(7,3e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A1818种 | B. | A2020种 | C. | A32A183A1010种 | D. | A22A1818种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(3ln2)>2f(3ln3) | B. | 3f(3ln2)与2f(3ln3)的大小不确定 | ||
| C. | 3f(3ln2)=2f(3ln3) | D. | 3f(3ln2)<2f(3ln3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com