
【题目】在锐角三角形ABC中,若![]() ,且满足关系式
,且满足关系式![]() ,则a+c的取值范围是( )
,则a+c的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由cosB![]() sinB=2,可得B=60°,由
sinB=2,可得B=60°,由![]() ,推导出b
,推导出b![]() ,再由余弦定理可得3ac=(a+c)2﹣3,由此能求出a+c的取值范围.
,再由余弦定理可得3ac=(a+c)2﹣3,由此能求出a+c的取值范围.
∵在锐角△ABC中,A、B、C分别为△ABC三边a,b,c所对的角.
![]() ,
,
∴2sin(B+30°)=2,
∴B=60°,
∵![]() ,
,
∴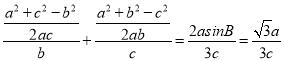 ,
,
解得b![]() ,
,
∴a+c![]() .
.
由余弦定理b2=a2+c2﹣2accosB,
即(![]() )2=a2+c2﹣2accos60°,
)2=a2+c2﹣2accos60°,
即3=(a+c)2﹣2ac﹣2ac![]() ,即3=(a+c)2﹣3ac,
,即3=(a+c)2﹣3ac,
即3ac=(a+c)2﹣3,即[(a+c)2﹣3]=3ac≤3[![]() (a+c)]2,
(a+c)]2,
令t=a+c,
即t2﹣3=3ac≤3(![]() )2,整理得t2≤12,
)2,整理得t2≤12,
即t的最大值2![]() 即a+c的最大值为2
即a+c的最大值为2![]() ,
,
综上,a+c的取值范围是(![]() ,2
,2![]() ].
].
故选:A.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABCD中,侧面PAD是正三角形,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
(1)求证:PC⊥AD.
(2)在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家放开计划生育政策,鼓励一对夫妇生育2个孩子.在某地区的100000对已经生育了一胎夫妇中,进行大数据统计得,有100对第一胎生育的是双胞胎或多胞胎,其余的均为单胞胎.在这99900对恰好生育一孩的夫妇中,男方、女方都愿意生育二孩的有50000对,男方愿意生育二孩女方不愿意生育二孩的有![]() 对,男方不愿意生育二孩女方愿意生育二孩的有
对,男方不愿意生育二孩女方愿意生育二孩的有![]() 对,其余情形有
对,其余情形有![]() 对,且
对,且![]() .现用样本的频率来估计总体的概率.
.现用样本的频率来估计总体的概率.
(1)说明“其余情形”指何种具体情形,并求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)该地区为进一步鼓励生育二孩,实行贴补政策:凡第一胎生育了一孩的夫妇一次性贴补5000元,第一胎生育了双胞胎或多胞胎的夫妇只有一次性贴补15000元.第一胎已经生育了一孩再生育了二孩的夫妇一次性再贴补20000元.这种补贴政策直接提高了夫妇生育二孩的积极性:原先男方或女方中只有一方愿意生育二孩的夫妇现在都愿意生育二孩,但原先男方、女方都不愿意生育二孩的夫妇仍然不愿意生育二孩.设![]() 为该地区的一对夫妇享受的生育贴补,求
为该地区的一对夫妇享受的生育贴补,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,一位游客来到某旅游城市,这里有甲、乙、丙三个著名的旅游景点,若这位游客游览这三个景点的概率分别是![]() ,且客人是否游览哪个景点互不影响,设
,且客人是否游览哪个景点互不影响,设![]() 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)记“![]() 时,不等式
时,不等式![]() 恒成立”为事件
恒成立”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
炼钢是一个氧化降碳的过程,由于钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:

(1)据统计表明,![]() 之间具有线性相关关系,请用相关系数r加以说明(
之间具有线性相关关系,请用相关系数r加以说明(![]()
![]() ,则认为y与x有较强的线性相关关系,否则认为没有较强的线性相关关系,r精确到0.001);
,则认为y与x有较强的线性相关关系,否则认为没有较强的线性相关关系,r精确到0.001);
(2)建立y关于x的回归方程(回归系数的结果精确到0.01);
(3)根据(2)中的结论,预测钢水含碳量为160个0.01%的冶炼时间.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据: ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为提升学生的英语学习能力,进行了主题分别为“听”、“说”、“读”、“写”四场竞赛.规定:每场竞赛的前三名得分分别为![]() ,
, ![]() ,
, ![]() (
(![]() ,且
,且![]() ,
, ![]() ,
, ![]() ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为
),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为![]() 分,乙最终得分为
分,乙最终得分为![]() 分,丙最终得分为
分,丙最终得分为![]() 分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
分,且乙在“听”这场竞赛中获得了第一名,则“听”这场竞赛的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了进一步提升基层党员自身理论素养,市委组织部举办了党建主题知识竞赛(满分120分),从参加竞赛的党员中采用分层抽样的方法抽取若干名党员,统计他们的竞赛成绩得到下面频率分布表:
成绩/分 |
|
|
|
|
|
频率 | 0.1 | 0.3 | 0.3 | 0.2 | 0.1 |
已知成绩在区间![]() 内的有
内的有![]() 人.
人.
(1)将成绩在![]() 内的定义为“优秀”,在
内的定义为“优秀”,在![]() 内的定义为“良好”,请将
内的定义为“良好”,请将![]() 列联表补充完整.
列联表补充完整.
男党员 | 女党员 | 合计 | |
优秀 | |||
良好 | 15 | ||
合计 | 25 |
(2)判断是否有![]() 的把握认为竞赛成绩是否优秀与性别有关?
的把握认为竞赛成绩是否优秀与性别有关?
(3)若在抽取的竞赛成绩为优秀的党员中任意抽取2人进行党建知识宣讲,求被抽取的这两人成绩都在![]() 内的概率.
内的概率.
附: ![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为6cm,该纸片上的正方形ABCD的中心为O.E,F,G,H为圆O上的点,△ABE,△BCF,△CDG,△ADH分别是以AB,BC,CD,DA为底边的等腰三角形.沿虚线剪开后,分别以AB,BC,CD,DA为折痕折起△ABE,△BCF,△CDG,△ADH,使得E,F,G,H重合得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的表面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com