
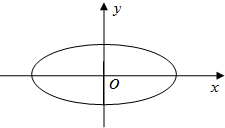
 如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点.
如图,中心在原点的椭圆的焦点在x轴上,长轴长为4,焦距为2$\sqrt{3}$,O为坐标原点.分析 (Ⅰ)设椭圆的方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,由$2c=2\sqrt{3}∴c=\sqrt{3}$继而求出b2=a2-c2=1,继而得出椭圆方程.
(Ⅱ)设直线斜率为k,则直线l的方程为:y=kx+2,由$\left\{\begin{array}{l}y=kx+2\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$得:(4k2+1)x2+16kx+12=0,由OA⊥OB得到x1x2+y1y2=0.代入求解即可.
解答 解:(Ⅰ)设椭圆的方程为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,∵2a=4∴a=2…(1分)
∵$2c=2\sqrt{3}∴c=\sqrt{3}$…(2分)∴b2=a2-c2=1…(3分)
所以,椭圆的方程为:$\frac{x^2}{4}+{y^2}=1$…(4分)
(Ⅱ)法一:假设存在过M(0,2)的直线l与椭圆交于A、B两个不同点,使以AB为直径的圆过原点,依题意可知OA⊥OB.
①当直线l的斜率不存在时,A、B分别为椭圆短轴的端点,不符合题意 …(5分)
②当直线l的斜率存在时,设为k,则直线l的方程为:y=kx+2
由$\left\{\begin{array}{l}y=kx+2\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$得:(4k2+1)x2+16kx+12=0…(6分)
令△>0,得:(16k)2-4•(4k2+1)•12=4k2-3>0∴${k^2}>\frac{3}{4}$…(7分)
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=-\frac{16k}{{4{k^2}+1}},{x_1}{x_2}=\frac{12}{{4{k^2}+1}}$…(8分)
又y1=kx1+2,y2=kx2+2∴${y_1}{y_2}=(k{x_1}+2)(k{x_2}+2)={k^2}{x_1}{x_2}+2k({x_1}+{x_2})+4$=$\frac{12}{{4{k^2}+1}}-\frac{{32{k^2}}}{{4{k^2}+1}}+4$=$\frac{{-20{k^2}}}{{4{k^2}+1}}+4=\frac{{4-4{k^2}}}{{4{k^2}+1}}$…(9分)
∵OA⊥OB∴x1x2+y1y2=0…(10分)∴$\frac{{12{k^2}}}{{4{k^2}+1}}+\frac{{4-4{k^2}}}{{4{k^2}+1}}=0$∴${k^2}=4>\frac{3}{4}$∴k=±2…(11分)
∴直线l的方程为:y=±2x+2,即2x-y+2=0或2x+y-2=0,
所以,存在过M(0,2)的直线与椭圆交于A、B两个不同点,使以AB为直径的圆过原点,其方程为:2x-y+2=0或2x+y-2=0.…(12分)
(Ⅱ)法二:假设存在过M(0,2)的直线l与椭圆交于A、B两个不同点,使以AB为直径的圆过原点,依题意可知OA⊥OB,设直线l的方程为:x=m(y-2)…(5分)
由$\left\{\begin{array}{l}x=m(y-2)\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$得:(m2+4)y2-4m2y+4m2-4=0…(6分)
令△>0,得:16m4-4•(m2+4)•(4m2-4)=64-48m2>0∴$0≤{m^2}<\frac{4}{3}$…(7分)
设A(x1,y1),B(x2,y2),则${y_1}+{y_2}=\frac{{4{m^2}}}{{{m^2}+4}},{y_1}{y_2}=\frac{{4{m^2}-4}}{{{m^2}+4}}$…(8分)
又${x_1}{x_2}=m({y_1}-2)•m({y_2}-2)={m^2}[{y_1}{y_2}-2({y_1}+{y_2})+4]$=$\frac{{12{m^2}}}{{{m^2}+4}}$…(9分)
∵OA⊥OB∴x1x2+y1y2=0…(10分)
∴$\frac{{12{m^2}}}{{{m^2}+4}}+\frac{{4{m^2}-4}}{{{m^2}+4}}=0$∴${m^2}=\frac{1}{4}<\frac{4}{3}$,
∴$m=±\frac{1}{2}$…(11分)∴所求直线的方程为:$x=±\frac{1}{2}(y-2)$,即2x-y+2=0或2x+y-2=0
所以,存在过M(0,2)的直线与椭圆交于A、B两个不同点,使以AB为直径的圆过原点,其方程为:2x-y+2=0或2x+y-2=0…(12分)
点评 本题主要考查直线与圆锥曲线的综合题,属于难度较大的题目,计算量大,在高考中经常在压轴题中出现.


科目:高中数学 来源: 题型:选择题
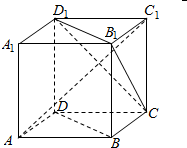
| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 平面ACC1A1⊥CB1D1 | D. | 异面直线AD与CB1所成的角为60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
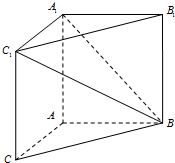 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).
已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.
已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com