
 (a>0,且a≠1)
(a>0,且a≠1) )+f(-
)+f(-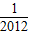 )的值;
)的值; )+f(-
)+f(- )的结构特点,先利用定义判断函数的奇偶性,由奇偶性的性质即可求得结果;
)的结构特点,先利用定义判断函数的奇偶性,由奇偶性的性质即可求得结果; 得:-1<x<1,所以f(x)的定义域为(-1,1),
得:-1<x<1,所以f(x)的定义域为(-1,1), =
= =-loga
=-loga =-f(x),∴f(x)为奇函数,
=-f(x),∴f(x)为奇函数, )+f(-
)+f(- )=0.
)=0. =
= ,
, ,
, ;
; .
. ,解得1<x<
,解得1<x< ,
, ).
).

 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
| log | (4x+1) 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| log | (4x+1)4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com