
【题目】过椭圆 ![]() =1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且
=1的右焦点F作斜率k=﹣1的直线交椭圆于A,B两点,且 ![]() 共线.
共线.
(1)求椭圆的离心率;
(2)当三角形AOB的面积S△AOB= ![]() 时,求椭圆的方程.
时,求椭圆的方程.
【答案】
(1)解:设AB:y=﹣x+c,直线AB交椭圆于两点,A(x1,y1),B(x2,y2),
 ,b2x2+a2(﹣x+c)2=a2b2,
,b2x2+a2(﹣x+c)2=a2b2,
(b2+a2)x2﹣2a2cx+a2c2﹣a2b2=0,
![]() ,
, ![]() ,
, ![]() =(x1+x2,y1+y2),与
=(x1+x2,y1+y2),与 ![]() =
= ![]() 共线,
共线,
可得3(y1+y2)﹣(x1+x2)=0,3(﹣x1+c﹣x2+c)﹣(x1+x2)=0 ![]()
(2)解:由a2=3b2,可设椭圆的方程为: ![]() ,c2=3b2﹣b2=2b2,
,c2=3b2﹣b2=2b2, ![]() ,
,
AB:y=﹣x+ ![]() b,
b,  ,可得:
,可得: ![]() ,
,
即 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
AB的距离为:|AB|= ![]() =
=  =
= ![]() ,
,
O到AB距离 ![]() .
.
![]() ,
,
椭圆方程为 ![]()
【解析】(1)设AB:y=﹣x+c,A(x1,y1),B(x2,y2),联立直线方程与椭圆方程,利用韦达定理,通过 ![]() 共线,即可求解椭圆的离心率.(2)利用第一问的结果a2=3b2,设椭圆的方程为:
共线,即可求解椭圆的离心率.(2)利用第一问的结果a2=3b2,设椭圆的方程为: ![]() ,AB:y=﹣x+
,AB:y=﹣x+ ![]() b,联立方程组,通过韦达定理求解|AB|,O到AB距离,通过三角形的面积,即可求解椭圆方程.
b,联立方程组,通过韦达定理求解|AB|,O到AB距离,通过三角形的面积,即可求解椭圆方程.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,给出下列四个命题: ①若|z1﹣z2|=0,则 ![]() =
= ![]() ②若z1=
②若z1= ![]() ,则
,则 ![]() =z2
=z2
③若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]() ④若|z1|=|z2|,则z12=z22
④若|z1|=|z2|,则z12=z22
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,是否存在折叠后的线段
,是否存在折叠后的线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(![]() )求三棱锥
)求三棱锥![]() 的体积的最大值,并求此时点
的体积的最大值,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.
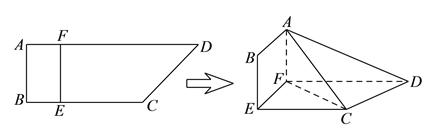
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过4(尾/立方米)时,
不超过4(尾/立方米)时,![]() 的值为
的值为![]() (千克/年);当
(千克/年);当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 达到
达到![]() (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因,![]() 的值为
的值为![]() (千克/年).
(千克/年).
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当养殖密度![]() 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com