
| A. | f(x)=|x+1|,g(x)=$\left\{\begin{array}{l}{x+1(x≥-1)}\\{-1-x(x<-1)}\end{array}\right.$ | B. | f(x)=$\frac{{x}^{2}-1}{x+1}$,g(x)=x-1 | ||
| C. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | D. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ |
分析 判断各组中所给的两个函数是否具有相同的定义域、值域、对应关系,从而作出判断.
解答 解:对于A,f(x)=|x+1|,定义域是R,g(x)=$\left\{\begin{array}{l}{x+1,(x≥1)}\\{-1-x,(x<-1)}\end{array}\right.$=|x+1|,定义域是R,定义域相同,对应关系也相同,是同一函数;
对于B,f(x)=$\frac{{x}^{2}-1}{x+1}$=x-1,定义域是{x|x≠-1},g(x)=x-1的定义域为R,定义域不同,不是同一函数;
对于C,f(x)=$\sqrt{{x}^{2}}$=|x|,定义域是R,g(x)=${(\sqrt{x})}^{2}$=x的定义域为[0,+∞),定义域不同,不是同一函数;
对于D,f(x)=x的定义域是R,g(x)=$\sqrt{{x}^{2}}$=|x|的定义域是R,对应关系不同,不是同一函数.
故选:A.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
| x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
| y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
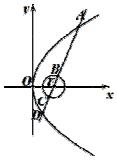 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com