
| A. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| B. | 命题“存在x∈R,x2-x>0”的否定是:“任意x∈R,x2-x≤0” | |
| C. | 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 | |
| D. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
分析 A.原命题的逆命题是“若a<b,则am2<bm2”是假命题,由于m=0时不成立;
B.利用“全称命题”的否定是“特称命题”即可判断出正误;
C.由“p或q”为真命题,可知:命题“p”和命题“q”至少有一个为真命题,即可判断出正误;
D.x∈R,则“x>1”是“x>2”的必要不充分条件,即可判断出正误.
解答 解:A.命题“若am2<bm2,则a<b”的逆命题是“若a<b,则am2<bm2”是假命题,m=0时不成立;
B.命题“存在x∈R,x2-x>0”的否定是:“任意x∈R,x2-x≤0”,正确;
C.“p或q”为真命题,则命题“p”和命题“q”至少有一个为真命题,因此不正确;
D.x∈R,则“x>1”是“x>2”的必要不充分条件,因此不正确.
故选:B.
点评 本题考查了简易逻辑的判定方法,考查了推理能力,属于中档题.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
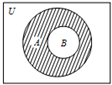 设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )
设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )| A. | {x|1<x<3} | B. | {x|1<x≤3} | C. | {x|1≤x<3} | D. | {x|1≤x≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com