
���� ��$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$���ó�$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$��P�ǡ�ABC�����ģ��жϢٴ���
��$\overrightarrow{OP}$=$\overrightarrow{OA}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|}}$�����ˣ�0�����ó�$\overrightarrow{AP}$=�ˣ�$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$����$\overrightarrow{AP}$���BAC��ƽ���������������ߣ��жϢ���ȷ��
��$\overrightarrow{OP}$=$\overrightarrow{OA}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|sinB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|sinC}}$�����ˣ�0�����ó�$\overrightarrow{AP}$=�ˣ�$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}$+$\frac{\overrightarrow{AC}}{|AC|sinC}$����$\overrightarrow{AP}$=$\frac{��}{AD}$��$\overrightarrow{AB}$+$\overrightarrow{AC}$�����жϢ���ȷ��
��$\overrightarrow{OP}$=$\overrightarrow{OA}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$�����ˣ�0�����ó�$\overrightarrow{AP}$=�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$����$\overrightarrow{AP}$•$\overrightarrow{BC}$=0���жϢ���ȷ��
��$\overrightarrow{OP}$=$\frac{{\overrightarrow{OB}+\overrightarrow{OC}}}{2}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$�����ˣ�0�����ó�EΪBC���е㣬��$\overrightarrow{EP}$=�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$����$\overrightarrow{EP}$��$\overrightarrow{BC}$���жϢ���ȷ��
��� �⣺���ڢ٣�����P����$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$����$\overrightarrow{AP}$=$\overrightarrow{PB}$+$\overrightarrow{PC}$��
��$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$����P�ǡ�ABC�����ģ�
���ABC�����IJ�һ����P��ļ����У��ٴ���
���ڢڣ�����P����$\overrightarrow{OP}$=$\overrightarrow{OA}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|}}$�����ˣ�0����
��$\overrightarrow{AP}$=�ˣ�$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$����
������$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$�ڡ�BAC��ƽ�����ϣ���$\overrightarrow{AP}$���BAC��ƽ���������������ߣ�
���ABC������������������P�㼯���У�����ȷ��
���ڢۣ�����P����$\overrightarrow{OP}$=$\overrightarrow{OA}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|sinB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|sinC}}$�����ˣ�0����
��$\overrightarrow{AP}$=�ˣ�$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}$+$\frac{\overrightarrow{AC}}{|AC|sinC}$����
����A��AD��BC������ΪD����|$\overrightarrow{AB}$|sinB=|$\overrightarrow{AC}$sinC=AD��
��$\overrightarrow{AP}$=$\frac{��}{AD}$��$\overrightarrow{AB}$+$\overrightarrow{AC}$��������$\overrightarrow{AB}$+$\overrightarrow{AC}$��BC�ߵ����߹��ߣ�
��ˡ�ABC������һ��������������P�㼯���У�����ȷ��
���ڢܣ�����P����$\overrightarrow{OP}$=$\overrightarrow{OA}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$�����ˣ�0����
��$\overrightarrow{AP}$=�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$������$\overrightarrow{AP}$•$\overrightarrow{BC}$=�ˣ�$\frac{\overrightarrow{AB}•\overrightarrow{BC}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}•\overrightarrow{BC}}{|\overrightarrow{AC}|cosC}$��=�ˣ�|$\overrightarrow{BC}$|-|$\overrightarrow{BC}$|��=0��
��$\overrightarrow{AP}$��$\overrightarrow{BC}$�����ABC�Ĵ���һ��������������P�㼯���У�����ȷ��
���ڢݣ�����P����$\overrightarrow{OP}$=$\frac{{\overrightarrow{OB}+\overrightarrow{OC}}}{2}$+�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$�����ˣ�0����
��$\frac{\overrightarrow{OB}+\overrightarrow{OC}}{2}$=$\overrightarrow{OE}$����EΪBC���е㣬��$\overrightarrow{EP}$=�ˣ�$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$����
�ɢ�֪��$\frac{{\overrightarrow{AB}}}{{|{AB}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{AC}|cosC}}$��•$\overrightarrow{BC}$=0����$\overrightarrow{EP}$•$\overrightarrow{BC}$=0����$\overrightarrow{EP}$��$\overrightarrow{BC}$��
��P��Ĺ켣Ϊ��E��BC�Ĵ��ߣ���BC���д��ߣ�
���ABC������һ��������������P�㼯�ϣ�����ȷ��
����ȷ�������Ǣڢۢܢݣ�
�ʴ�Ϊ���ڢۢܢݣ�
���� �����ۺϿ�����������ʽ�������ε����ġ����ġ����ġ����ĵ����ʼ���������������������㣬���������ν�ϵ�˼�뷽�����������⣮


 ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д� A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-13��-1] | B�� | ��-�ޣ�-1] | C�� | [-13��+�ޣ� | D�� | [1��13] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|-2��x��2} | B�� | {x|-2��x��4} | C�� | {x|0��x��2} | D�� | {x|2��x��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{43}{74}$ | B�� | $\frac{74}{43}$ | C�� | $\frac{39}{23}$ | D�� | $\frac{23}{39}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
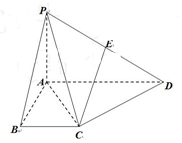 ����ͼ��ʾ������P-ABCD�У���֪PA��ƽ��ABCD��AD��BC����BAD=90�㣬PA=AB=BC=1��AD=2��EΪPD���е㣮
����ͼ��ʾ������P-ABCD�У���֪PA��ƽ��ABCD��AD��BC����BAD=90�㣬PA=AB=BC=1��AD=2��EΪPD���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com