
���� ��1��ֱ�����ùŵ�����ʵ�����n��ʾһ�������н��ĸ���p��
��2���Ǵӿڴ�������������ÿ����������Żأ�ǡ��һ���н��ĸ���Ϊm���г����̼�����m�����ֵ��
��3���ڣ�2�������½�5������ȫ��ȡ����ʣ�µ�n������ȫ�������±�ǣ��Ʊ�ʾ��ȡ��ı�ţ�������ʣ��õ��ֲ��У�Ȼ����������뷽�
��� ��12�֣�
�⣨1��$p=\frac{c_n^1c_5^1}{{c_{n+5}^2}}=\frac{10n}{��n+5����n+4��}$
��2����ÿ���н��ĸ���Ϊp����������ǡ��һ���н��ĸ����ǣ�$m={p_3}��1��=c_3^1p{��1-p��^2}=\frac{3}{2}2p��1-p����1-p����\frac{3}{2}{��\frac{2p+1-p+1-p}{3}��^3}=\frac{4}{9}$
���ҽ���2p=1-p��$p=\frac{1}{3}$ʱ��mȡ�����ֵ$\frac{4}{9}$��
��$p=\frac{1}{3}$ʱ��$\frac{10n}{{{n^2}+9n+20}}=\frac{1}{3}⇒n=20$
��3���Ƶ�ֵ�ֱ�Ϊ��0��1��2��3��4������0�ŵ���10����������ȡһ����20��ȡ���������ǵȿ��ܵĹʦεķֲ�����
| �� | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{1}{2}$ | $\frac{1}{20}$ | $\frac{2}{20}$ | $\frac{3}{20}$ | $\frac{4}{20}$ |
���� ��С����Ҫ���麯�������Ե�Ӧ�á��ȿ����¼��ĸ��ʡ���ɢ����������������뷽��Ȼ���֪ʶ������ɢ��������������IJ��裺��ȷ����ɢ��������� ��ȡֵ����д���ֲ��У������ֲ��е���ȷ�����һ�����и��ʵĺ��Ƿ�Ϊ1�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2014 | B�� | 2015 | C�� | -2015 | D�� | -2016 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
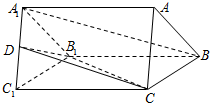 ��ͼ����������ABC-A1B1C1�У���ABC�ǵȱ������Σ�BC=CC1=4��D��A1C1�е㣮
��ͼ����������ABC-A1B1C1�У���ABC�ǵȱ������Σ�BC=CC1=4��D��A1C1�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com