
分析 (1)由a≥2,分子有理化求得$\sqrt{a+1}$-$\sqrt{a}$=$\frac{1}{\sqrt{a+1}+\sqrt{a}}$,$\sqrt{a-1}$-$\sqrt{a-2}$=$\frac{1}{\sqrt{a-1}+\sqrt{a-2}}$,利用不等式的性质,即可得证;
(2)利用“1”代换,$\frac{1}{a}$+$\frac{1}{b}$=(a+b)×($\frac{1}{a}$+$\frac{1}{b}$),展开利用基本不等式的性质可知求得则$\frac{1}{a}+\frac{1}{b}>4$.
解答 证明:(1)由a≥2,$\sqrt{a+1}$-$\sqrt{a}$=$\frac{1}{\sqrt{a+1}+\sqrt{a}}$,
$\sqrt{a-1}$-$\sqrt{a-2}$=$\frac{1}{\sqrt{a-1}+\sqrt{a-2}}$,
$\sqrt{a}$>$\sqrt{a-2}$≥0,$\sqrt{a+1}$>$\sqrt{a-1}$>0,
两式相加可得:$\sqrt{a}$+$\sqrt{a+1}$>$\sqrt{a-1}$+$\sqrt{a-2}$>0,
∴$\frac{1}{\sqrt{a+1}+\sqrt{a}}$<$\frac{1}{\sqrt{a-1}+\sqrt{a-2}}$,
∴$\sqrt{a+1}-\sqrt{a}<\sqrt{a-1}-\sqrt{a-2}$;
(2)$\frac{1}{a}$+$\frac{1}{b}$=(a+b)×($\frac{1}{a}$+$\frac{1}{b}$)=2+$\frac{b}{a}$+$\frac{a}{b}$>2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=4,
∴$\frac{1}{a}+\frac{1}{b}>4$.
点评 本题考查不等式的证明,考查不等式的性质及基本不等式的应用,考查推理能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{8}$ | B. | $\frac{{\sqrt{2}}}{6}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
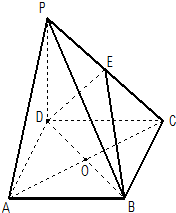 如图,在四棱锥P-ABCD中,底面ABCD是棱长为a正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC中点,AC与BD交于O点.
如图,在四棱锥P-ABCD中,底面ABCD是棱长为a正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC中点,AC与BD交于O点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
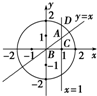 直线x=1,y=x,将圆x2+y2=4分成A,B,C,D四个区域,如图用五种不同的颜色给他们涂色,要求共边的两区域颜色互异,每个区域只涂一种颜色,共有多少种不同的涂色方法?
直线x=1,y=x,将圆x2+y2=4分成A,B,C,D四个区域,如图用五种不同的颜色给他们涂色,要求共边的两区域颜色互异,每个区域只涂一种颜色,共有多少种不同的涂色方法?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2012 | B. | 2012 | C. | 4024 | D. | 4022 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com