
| A. | $\frac{{\sqrt{2}}}{8}$ | B. | $\frac{{\sqrt{2}}}{6}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 由题意,直线l:y=k(x+2)过定点(-2,0),曲线$Γ:\sqrt{1-{{(x-1)}^2}}-y=0$,即(x-1)2+y2=1(y≥0),表示以(1,0)为圆心,1为半径的上半圆,求出直线l与曲线Γ有两个交点的充要条件,以长度为测度,即可求出概率.
解答 解:由题意,直线l:y=k(x+2)过定点(-2,0),曲线$Γ:\sqrt{1-{{(x-1)}^2}}-y=0$,即(x-1)2+y2=1(y≥0),表示以(1,0)为圆心,1为半径的上半圆,
直线与半圆相切时,k=$\frac{1}{\sqrt{9-1}}$=$\frac{\sqrt{2}}{4}$,∴直线l与曲线Γ有两个交点的充要条件为0<k<$\frac{\sqrt{2}}{4}$,
∴所求概率P=$\frac{\frac{\sqrt{2}}{4}-0}{1-(-1)}$=$\frac{\sqrt{2}}{8}$,
故选A.
点评 本题考查概率知识的运用,考查直线与圆的位置关系,考查学生的计算能力,确定直线l与曲线Γ有两个交点的充要条件是关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 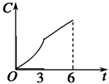 | B. | 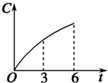 | C. | 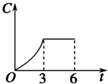 | D. | 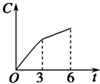 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | -2015 | D. | -2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
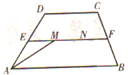 如图,已知四边形ABCD是等腰梯形,E、F是腰AD、BC中点,M、N是EF两个三等分点,下底是上底2倍,若向量$\overrightarrow{AB}$=$\overrightarrow{a}$,向量$\overrightarrow{BC}$=$\overrightarrow{b}$,则向量$\overrightarrow{AM}$用$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,已知四边形ABCD是等腰梯形,E、F是腰AD、BC中点,M、N是EF两个三等分点,下底是上底2倍,若向量$\overrightarrow{AB}$=$\overrightarrow{a}$,向量$\overrightarrow{BC}$=$\overrightarrow{b}$,则向量$\overrightarrow{AM}$用$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )| A. | $\frac{1}{2}$($\overrightarrow{a}+\overrightarrow{b}$) | B. | -$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$ | D. | $\frac{1}{3}\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com