设x2+ax+b2=0是关于x的一元二次方程
(1)若a,b是分别从{1,2,3,4},{0,1,2}中任取的数字,求方程有实根的概率.
(2)若a,b都是从区间[-1,1]中任取的一个数字,求方程有实根的概率.
【答案】
分析:根据题意,由一元二次方程的性质,可得x
2+ax+b
2=0有实根的充要条件为a
2≥4b
2,
(1)由题意分析可得,这是古典概型,由a、b分别从{1,2,3,4},{0,1,2}中任取的数字,易得一共可以得到12个不同方程,对a分情况讨论,可得满足a
2≥4b
2的全部情况数目,结合古典概型公式,计算可得答案;
(2)由题意分析可得,这是几何概型,将-1≤a≤1,-1≤b≤1表示为平面区域,进而可得其中满足a
2≥4b
2的区域的面积,由几何概型公式,计算可得答案.
解答:解:根据题意,方程x
2+ax+b
2=0有实根的充要条件为a
2≥4b
2
(1)由题意,a,b是分别从{1,2,3,4},{0,1,2}中任取的数字;
则a有4种取法,b有3种取法,共有12不同的情况,可以得到12个不同方程,
当a=1时,b=0,满足a
2≥4b
2,有1种情况满足方程有实根;
当a=2时,b=0、1,满足a
2≥4b
2,有2种情况满足方程有实根;
当a=3时,b=0,1;满足a
2≥4b
2,有2种情况满足方程有实根;
当a=4时,b=0、1、2,满足a
2≥4b
2,有3种情况满足方程有实根;
共有1+2+2+3=8种情况满足方程有实根,
∴
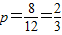
;
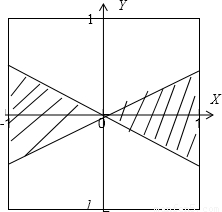
(2)由题意得:-1≤a≤1,-1≤b≤1,右图的正方形区域,
∵△=a
2-4b
2≥0,
∴(a+2b)(a-2b)≥0,即图中阴影区域,
由图可知
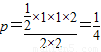
.
点评:本题考查几何概型和古典概型,放在一起的目的是把两种概型加以比较,注意两者的不同.


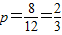 ;
;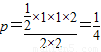 .
.
