
���� ��1��ѡ�����ȷ���һ���Żݣ�����Ҫ��������һ���������ɴ������������һ���˿ͱ�ѡ��һ���Żݵĸ��ʣ�
��2����ѡ��һ�����踶��9.4��Ԫ����ѡ�������踶����ΪX��Ԫ����X���ܵ�ȡֵΪ6��7��8��10���ֱ������Ӧ�ĸ��ʣ��Ӷ����X����ѧ�������ɴ˵õ�ѡ��ڶ��ַ��������㣮
��� �⣺��1��ѡ�����ȷ���һ���Żݣ�
����Ҫ��������һ��������
��˿Ͳ����ۼ�����û����������Ϊ�¼�A��
��$P��A��=\frac{2��2��3}{4��4��4}=\frac{3}{16}$��
���������$P=1-P��A��P��A��=1-{��\frac{3}{16}��^2}=\frac{247}{256}$����4�֣�
��2����ѡ��һ�����踶��10-0.6=9.4����Ԫ���� 5�֣�
��ѡ�������踶����ΪX��Ԫ��
��X���ܵ�ȡֵΪ6��7��8��10��$P��X=6��=\frac{2��2��1}{4��4��4}=\frac{1}{16}��P��X=7��=\frac{2��2��3+2��2��1+2��2��1}{4��4��4}=\frac{5}{16}$��$P��X=8��=\frac{2��2��3+2��2��3+2��2��1}{4��4��4}=\frac{7}{16}$��$P��X=10��=\frac{3}{16}$����9�֣�
��X�ķֲ���Ϊ
| X | 6 | 7 | 8 | 10 |
| P | $\frac{1}{16}$ | $\frac{5}{16}$ | $\frac{7}{16}$ | $\frac{3}{16}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ������������������֤������������������������������˼�롢ת������˼�롢����˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | 1 | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
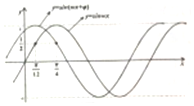
| A�� | ��x������ƽ��$\frac{��}{6}$����λ | B�� | ��x������ƽ��$\frac{��}{3}$����λ | ||
| C�� | ��x������ƽ��$\frac{��}{6}$����λ | D�� | ��x������ƽ��$\frac{��}{6}$����λ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-16���ȣ�$\frac{1}{3}$��+�ޣ� | B�� | [-16��$\frac{1}{3}$] | C�� | ��-16��$\frac{1}{3}$�� | D�� | ��$\frac{1}{3}$��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com