
| A. | $\frac{16}{17}$ | B. | $\frac{36}{5}$ | C. | $\frac{26}{5}$ | D. | $\frac{196}{53}$ |
分析 根据题意画出图形,由图形和同角三角函数的基本关系求出正方形面积.
解答 解:如果过点P(1,0),Q(2,0),R(4,0),S(8,0)作四条直线构成一个正方形,
过P点的必须和过Q,R,S的其中一条直线平行和另外两条垂直,
假设过P点和Q点的直线相互平行时,如图 ,
,
设直线PC与x轴正方向的夹角为θ,再过Q作它的平行线QD,过R、S作它们的垂线RB、SC,过点A作x轴的平行线分别角PC、SC于点M、N,
则AB=AMsinθ=PQsinθ=sinθ,AD=ANcosθ=RScosθ=4cosθ,
因为AB=AD,所以sinθ=4cosθ,则tanθ=4,
所以正方形ABCD的面积S=AB•AD=4sinθcosθ=$\frac{4sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{4tanθ}{ta{n}^{2}θ+1}$=$\frac{16}{17}$,
同理可求,当直线PC和过R的直线平行时正方形ABCD的面积S为$\frac{36}{5}$,
当直线PC和过S点的直线平行时正方形ABCD的面积S为$\frac{193}{53}$,
故选:C.
点评 本题考查同角三角函数的基本关系,以及数形结合思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
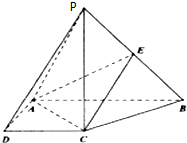 如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | m | -4 | -6 | -6 | -4 | n | 6 |
| A. | (-3,-1)和(2,4) | B. | (-3,-1)和(-1,1) | C. | (-1,1)和(1,2) | D. | (-1,3)和(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象关于直线x=$\frac{5π}{12}$对称 | B. | f(x)的图象关于y轴对称 | ||
| C. | f(x)的最小正周期为2π | D. | f(x)在区间(0,$\frac{π}{3}$)单调递增 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com