练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四面体ABCD中，与都是边长为8的正三角形，点O是线段BC的中点.

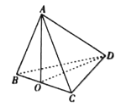
    （1）证明：.

    （2）若为锐角，且四面体ABCD的体积为求侧面ACD的面积.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）通过正三角形的性质易得，，由线面垂直判定定理可得平面AOD，最后由线垂直于某个面线将垂直于该面内所有直线即可得结果；

    （2）过点D作，垂足为E，易得平面平面ABC，根据面面垂直性质定理可得平面ABC，由四面体的体积可得，接着算出，根据三角形面积公式即可得结果.

    （1）证明：是正三角形，.

    ∵也是正三角形，

    ，且

    平面AOD.

    又平面AOD，

    .

    （2）过点D作，垂足为E.

    ∵平面ADO，且平面ABC，

    平面平面ABC

    又平面平面，平面ABC.

    四面体ABCD的体积为，的面积，

    ，.

    又，

    ，

    ，

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知定义域为的函数是奇函数，为指数函数且的图象过点.

    （1）求实数n的值并写出的表达式；

    （2）若对任意的，不等式恒成立，求实数t的范围；

    （3）若方程恰有4个互异的实数根，求实数a的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S＝ABCD的底面是正方形，SD⊥平面ABCD,SD＝AD＝a,点E是SD上的点，且DE＝a(0<≦1). w.w.w..c.o.m

    (Ⅰ)求证：对任意的（0、1），都有AC⊥BE:

    (Ⅱ)若二面角C-AE-D的大小为600C，求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）判断函数的零点的个数并说明理由；

    （2）求函数零点所在的一个区间，使这个区间的长度不超过；

    （3）若，对于任意的，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列的前项和为，，且，，成等差数列.

    (1)求的值，并证明为等比数列；

    (2)设，若对任意的，不等式恒成立，试求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为弘扬中华传统文化，学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查，小明同学阅读两类读物的阅读量统计如下：

    小明阅读“经典名著”的阅读量（单位：字）与时间t（单位：分钟）满足二次函数关系，部分数据如下表所示；

    t

    0

    10

    20

    30

    0

    2700

    5200

    7500

    阅读“古诗词”的阅读量（单位：字）与时间t（单位：分钟）满足如图1所示的关系.

    （1）请分别写出函数和的解析式；

    （2）在每天的一小时课外阅读活动中，小明如何分配“经典名著”和“古诗词”的阅读时间，使每天的阅读量最大，最大值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆：关于直线：对称的圆为．

    （Ⅰ）求圆的方程；

    （Ⅱ）过点作直线与圆交于，两点，是坐标原点，是否存在这样的直线，使得在平行四边形（和为对角线）中？若存在，求出所有满足条件的直线的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （Ⅰ）求曲线在处的切线方程；

    （Ⅱ）当时，求的零点个数；

    （Ⅲ）若函数在上是增函数，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数在上的最小值和最大值；

    （2）当时，讨论函数的单调性.

    查看答案和解析>>

    同步练习册答案