
已知函数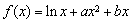 (其中
(其中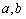 为常数且
为常数且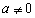 )在
)在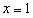 处取得极值.
处取得极值.
(I) 当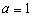 时,求
时,求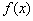 的单调区间;
的单调区间;
(II) 若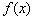 在
在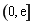 上的最大值为
上的最大值为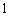 ,求
,求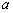 的值.
的值.
(I)单调递增区间为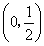 ,
,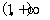 单调递减区间为
单调递减区间为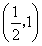 (II)
(II) 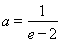 或
或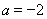
【解析】(I)因为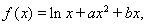 所以
所以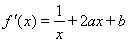 ………………2分
………………2分
因为函数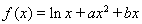 在
在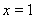 处取得极值
处取得极值
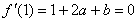 ………………3分
………………3分
当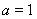 时,
时,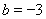 ,
,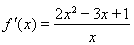 ,
,
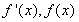 随
随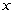 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| 极大值 |
| 极小值 |
|
所以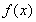 的单调递增区间为
的单调递增区间为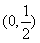 ,
,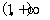 单调递减区间为
单调递减区间为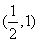 ………………6分
………………6分
(II)因为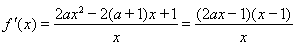
令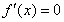 ,
,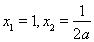 ………………7分
………………7分
因为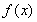 在
在 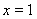 处取得极值,所以
处取得极值,所以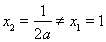
当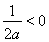 时,
时,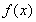 在
在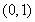 上单调递增,在
上单调递增,在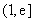 上单调递减
上单调递减
所以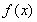 在区间
在区间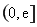 上的最大值为
上的最大值为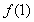 ,令
,令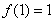 ,解得
,解得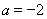 ………………9分
………………9分
当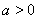 ,
,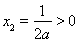
当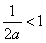 时,
时,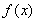 在
在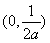 上单调递增,
上单调递增,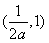 上单调递减,
上单调递减,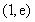 上单调递增
上单调递增
所以最大值1可能在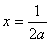 或
或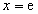 处取得
处取得
而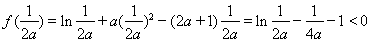
所以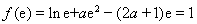 ,解得
,解得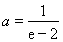 ………………11分
………………11分
当 时,
时,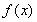 在区间
在区间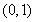 上单调递增,
上单调递增,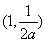 上单调递减,
上单调递减,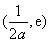 上单调递增
上单调递增
所以最大值1可能在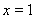 或
或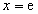 处取得
处取得
而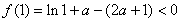 所以
所以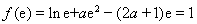 ,
,
解得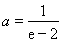 ,与
,与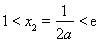 矛盾………………12分
矛盾………………12分
当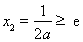 时,
时,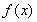 在区间
在区间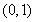 上单调递增,在
上单调递增,在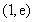 单调递减,
单调递减,
所以最大值1可能在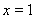 处取得,而
处取得,而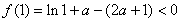 ,矛盾
,矛盾
综上所述,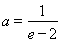 或
或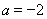 . ………………13分
. ………………13分


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷(解析版) 题型:解答题
2×2矩阵M对应的变换将点(1,2)与(2,0)分别变换成点(7, 10)与(2,4).
(1)求矩阵M的逆矩阵M-1.
(2)设直线l在变换M作用下得到了直线m:2x-y=4,求l的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:选择题
已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )
(A)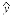 =1.23x+4
=1.23x+4
(B)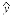 =1.23x+5
=1.23x+5
(C) =1.23x+0.08
=1.23x+0.08
(D) =0.08x+1.23
=0.08x+1.23
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:填空题
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.设ξ为取出的4个球中红球的个数,则P(ξ=2)= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
设随机变量ξ的概率分布为P(ξ=i)=a( )i,i=1,2,3,则a的值是( )
)i,i=1,2,3,则a的值是( )
(A)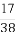 (B)
(B)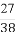 (C)
(C)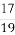 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数 ,
, 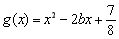 .
.
(Ⅰ)当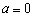 时,求曲线
时,求曲线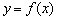 在点
在点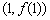 处的切线方程;
处的切线方程;
(Ⅱ)当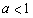 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当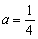 时,函数
时,函数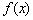 在
在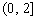 上的最大值为
上的最大值为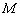 ,若存在
,若存在 ,使得
,使得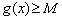 成立,求实数b的取值范围.
成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:选择题
某产品在某零售摊位上的零售价x(元)与每天的销售量y(个)统计如下表:据上表可得回归直线方程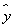 =b
=b +a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )
+a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )

A.48 B.49 C.50 D.51
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com