
已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )
(A)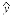 =1.23x+4
=1.23x+4
(B)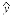 =1.23x+5
=1.23x+5
(C)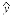 =1.23x+0.08
=1.23x+0.08
(D)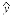 =0.08x+1.23
=0.08x+1.23
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷(解析版) 题型:解答题
已知在一个2×2矩阵M的变换作用下,点A(1,2)变成了点A'(4,5),点B(3,-1)变成了点B'(5,1).
(1)求2×2矩阵M.
(2)若在2×2矩阵M的变换作用下,点C(x,0)变成了点C'(4,y),求x,y.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
设一次试验成功的概率为p,进行100次独立重复试验,当p=_______时,成功次数的标准差的值最大,其最大值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:填空题
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单元:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: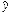 =0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
=0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
从原点O引直线交直线2x+4y-1=0于点M,P为OM上一点,已知OP·OM=1,求P点所在曲线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:解答题
一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于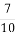 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数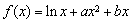 (其中
(其中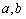 为常数且
为常数且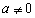 )在
)在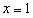 处取得极值.
处取得极值.
(I) 当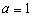 时,求
时,求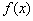 的单调区间;
的单调区间;
(II) 若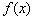 在
在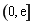 上的最大值为
上的最大值为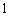 ,求
,求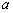 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
如图,在棱长为 的正方体
的正方体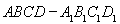 中,点
中,点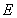 是棱
是棱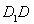 的中点,点
的中点,点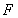 在棱
在棱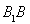 上,且满足
上,且满足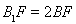 .
.
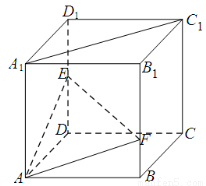
(1)求证: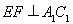 ;
;
(2)在棱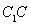 上确定一点
上确定一点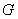 ,使
,使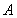 、
、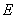 、
、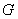 、
、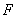 四点共面,并求此时
四点共面,并求此时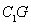 的长;
的长;
(3)求平面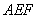 与平面
与平面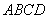 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com