
已知函数f(x)=-x3+x2,g(x)=aln x,a∈R.
(1)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求a的取值范围;
(2)设F(x)=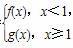 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
解 (1)由g(x)≥-x2+(a+2)x,得(x-ln x)a≤x2-2x.
由于x∈[1,e],ln x≤1≤x,且等号不能同时取得,所以ln x<x,x-ln x >0.
>0.
从而a≤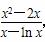 恒成立,a≤
恒成立,a≤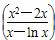 min.(4分)
min.(4分)
设t(x)=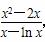 ,x∈[1,e].求导,得t′(x)=
,x∈[1,e].求导,得t′(x)=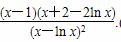 .(6分)
.(6分)
x∈[1,e],x-1≥0,ln x≤1,x+2-2ln x>0,从而t′(x)≥0,t(x)在[1,e]上为增函数.
所以t(x)min=t(1)=-1,所以a的取值范围是(-∞,- 1].(8分
1].(8分 )
)
(2)F(x)=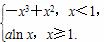
设P(t,F(t))为 曲线y=F(x)上的任意一点.
曲线y=F(x)上的任意一点.
假设曲线y=F(x)上存在一点Q(-t,F(-t)),使∠POQ为钝角,
则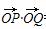 <0.(10分)
<0.(10分)
① 若t≤-1,P(t,-t3+t2),Q(-t,aln(-t)),
若t≤-1,P(t,-t3+t2),Q(-t,aln(-t)),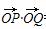 =-t2+aln(-t)·(-t3+t2).
=-t2+aln(-t)·(-t3+t2).
由于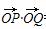 <0恒成立,a(1-t)ln(-t)<1.
<0恒成立,a(1-t)ln(-t)<1.
当t=-1时,a(1-t)ln(-t)<1恒成立.
当t<-1时,a<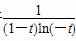 恒成立.由于
恒成立.由于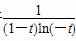 >0,所以a≤0.(12分)
>0,所以a≤0.(12分)
②若-1<t<1,且t≠0,P(t,-t3+t2),Q(-t,t3+t2),则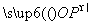 ·
·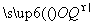 =-t2+(-t3+t2)·(t3+t2)<0,
=-t2+(-t3+t2)·(t3+t2)<0,
即t4-t2+1>0对-1<t<1,且t≠0恒成立.(14分)
③当t≥1时,同①可得a≤0 .
.
综上所述,a的取值范围是(-∞,0].(16分)


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
八个一样的小球按顺序排成一排,涂上红、白两种颜色,5个涂红色,三个涂白色,恰好有三个连续的小球涂红色,则涂法共有
A.24种 B.30种 C.20种 D.36种
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=aln x= (a为常数
(a为常数 ).
).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,求a的值;
(2)求函数f(x)的单调区间;
(3)当x≥1时,f(x)≤2x-3恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{bn}满足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-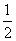 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
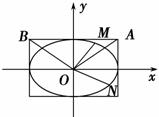
如图,已知椭圆C: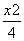 +y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
(1)设P是椭圆C上任意一点,若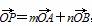 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两上动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的 面积是否为定值,说明理由.
面积是否为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列有关命题的说法正确的是( )
A.命题“若x2 =4,则x=2”的否命题为:“若x2 =4,则x≠2”
B.“x=2”是“x2—6x+8=0”的必要不充分条件
C.命题“若x=y,则cosx=cosy”的逆否命题为真命题
D.命题“存在x∈R,使得x2+x+3>0”的否定是:“对于任意的x∈R,均有
x2 +x+3<0"
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线的方程为 ,直线
,直线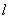 的方程为
的方程为 ,点A
,点A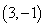 关于直线
关于直线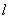 的对称点在抛物线上.
的对称点在抛物线上.
(1)求抛物线的方程;
(2)已知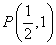 ,点
,点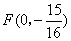 是抛物线的焦点,M是抛物线上的动点,求
是抛物线的焦点,M是抛物线上的动点,求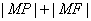 的最小值及此时点M的坐标;
的最小值及此时点M的坐标;
(3)设点B、C是抛物线上的动点,点D是抛物线与 轴正半轴交点,△BCD是以D为直角顶点的直角三角形.试探究直线BC是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
轴正半轴交点,△BCD是以D为直角顶点的直角三角形.试探究直线BC是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com