
设m,n是空间中的两条直线,α,β是空间中的两个平面,则下列选项中不正确的是( )
A.当n⊥α时,“n⊥β”是“α∥β”的充要条件
B.当m⊂α时,“m⊥β”是“α⊥β”的充分不必要条件
C.当m⊂α时,“n∥α”是“m∥n”的必要不充分条件
D.当m⊂α时,“n⊥α”是“m⊥n”的充分不必要条件
科目:高中数学 来源: 题型:
用反证法证明命题“三角形的三个内角至少有一个不大于60°”时,应假设( )
A.三个内角都不大于60°
B.三个内角都大于60°
C.三个内角至多有一个大于60°
D.三个内角至多有两个大于60°
查看答案和解析>>
科目:高中数学 来源: 题型:
A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知四棱锥P ABCD的三视图如图K4014所示,其中主视图和左视图是直角三角形,俯视图是正方形,E是侧棱PC上的动点.
(1)求四棱锥P ABCD的体积.
(2)不论点E在何位置,是否都有BD⊥AE?证明你的结论.
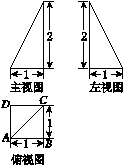
图K4014
查看答案和解析>>
科目:高中数学 来源: 题型:
已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列结论中正确的有________.
①若m∥α,n∥α,则m∥n;
②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,m∥β,则α∥β;
④若m⊥α,n⊥α,则m∥n.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图K424所示,四棱锥P ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,BE⊥PC于点E,且BE= a,试在AB上找一点F,使EF∥平面PAD.
a,试在AB上找一点F,使EF∥平面PAD.
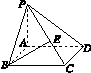
图K424
查看答案和解析>>
科目:高中数学 来源: 题型:
已知平面α,β和直线m,给出下列条件:①m∥α;②m⊥α;③m⊂α;④α⊥β;⑤α∥β.
(1)当满足条件________时,有m∥β;
(2)当满足条件________时,有m⊥β.(填所选条件的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知正方体ABCD A1B1C1D1中,点E为A1C1的中点,若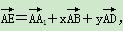 ,则x,y的值分别为( )
,则x,y的值分别为( )
A.x=1,y=1 B.x=1,y=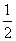
C.x=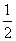 ,y=
,y=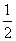 D.x=
D.x=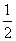 ,y=1
,y=1
查看答案和解析>>
科目:高中数学 来源:2016届四川省成都市高三11月段测三文科数学试卷(解析版) 题型:解答题
设△ABC的三个内角A,B,C所对的边长分别为a,b,c.平面向量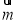 =(cosA,cosC),
=(cosA,cosC),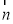 =(c,a),
=(c,a),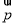 =(2b,0),且
=(2b,0),且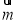 ·(
·(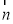 -
-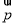 )=0
)=0
(1)求角A的大小;
(2)当|x|≤A时,求函数f(x)=sinxcosx+sinxsin(x-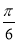 )的值域.
)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com