（本小题12分）
在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且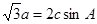
(1)求角C的大小；
（2）若c＝
,且△ABC的面积为
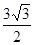
,求a＋b的值。
科目：高中数学 来源： 题型：解答题
(本题满分14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分.
（文）某种型号汽车的四个轮胎半径相同，均为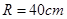
，该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是：水面不能超过它的底盘高度. 如图所示：某处有一“坑形”地面，其中坑
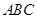形成顶角为
的等腰三角形，且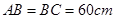
，如果地面上有
(
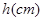)高的积水(此时坑内全是水，其它因素忽略不计).
（1）当轮胎与
、
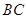同时接触时，求证：此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为
；
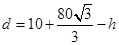(2) 假定该汽车能顺利通过这个坑(指汽车在过此坑时，符合涉水安全要求)，求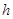
的最大值.
(精确到1cm).
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分13分）我炮兵阵地位于地面A处，两观察所分别位于地面点C和D处，已知CD=6
，∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时，测得∠BCD=30°，∠BDC=15°(如图），求炮兵阵地到目标的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）5.
，并利用正弦定理化简，根据sinA不为0，可得出sinC的值，由三角形为锐角三角形，得出C为锐角，利用特殊角的三角函数值即可求出C的度数；
求得a+b的值．.
…………3分
……………7分
.
所对的分别是
。已知
。（1）求
的值；
的值。
的内角
的对边分别为
的大小；
，
，求
．
中，角
的对边分别为
，且
.
的值；
，且
，求
的值.
中，角A、B、C所对的边分别是 a,b,c且a="2," 
的值.
=3，求b,c的值.
的值.
分别为
三个内角
的对边，
，（1）求
； （2）若
，
；求
.