
分析 (1)由题意,A=B,A=(a,5+a],B={x|-$\frac{a}{2}$<x≤6},即可得出结论;
(2)若A∪B=A,则B⊆A,分类讨论,可得结论.
解答 解:(1)由题意,A=B,A=(a,5+a],B={x|-$\frac{a}{2}$<x≤6}
∴$\left\{\begin{array}{l}{a=-\frac{a}{2}}\\{5+a=6}\end{array}\right.$,无解,
∴不存在实数a,使∁R(A∪B)=(∁RA)∪(∁RB);
(2)若A∪B=A,则B⊆A,
∴B=∅,-$\frac{a}{2}≥6$,∴a≤-12,
B≠∅,a>-12时$\left\{\begin{array}{l}{-\frac{a}{2}≥a}\\{5+a≥6}\end{array}\right.$,∴无解,
综上所述a≤-12.
点评 本题考查集合的关系与运算,考查学生分析解决问题的能力,属于中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:填空题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{100}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{25}-\frac{y^2}{100}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
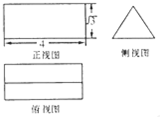 一个正棱柱(底面是正三角形、侧棱垂直于底面的棱柱)的三视图如图所示,则该三棱柱的表面积等于( )
一个正棱柱(底面是正三角形、侧棱垂直于底面的棱柱)的三视图如图所示,则该三棱柱的表面积等于( )| A. | 2$\sqrt{3}$+12 | B. | 2$\sqrt{3}$+24 | C. | 2$\sqrt{3}$+12 | D. | 6$\sqrt{3}$+24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示为棱长为1的正方体的表面展开图,在原正方体中,给出下列四个结论:
如图所示为棱长为1的正方体的表面展开图,在原正方体中,给出下列四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 患慢性气管炎 | 未患慢性气管炎 | 合计 | |
| 吸烟 | 20 | 20 | 40 |
| 不吸烟 | 5 | 55 | 60 |
| 合计 | 25 | 75 | 100 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com