
某高校共有学生15 000人,其中男生10 500人,女生4 500人,为调查该校学生每周平均体育运动的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4], (4,6], (6,8], (8,10], (10,12],估计该校学生每周平均体育运动时间超过4小时的概率;

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
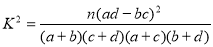
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(1) 90;(2) 0.75;(3) 有.
【解析】
试题分析:(1)由分层抽样方法可知每层应抽取的比例相同且为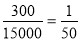 ,所以女生应抽取人数就等于女生总人数4 500 乘以抽取比例;(2) 该校学生每周平均体育运动时间超过4小时的概率等于1减去[0,2],(2,4]矩形方块的高度之和乘以组距2; (3)首先应计算出在样本数据的300人中,每周平均体育运动时间超过4小时的男生人数和女生人数,列出
,所以女生应抽取人数就等于女生总人数4 500 乘以抽取比例;(2) 该校学生每周平均体育运动时间超过4小时的概率等于1减去[0,2],(2,4]矩形方块的高度之和乘以组距2; (3)首先应计算出在样本数据的300人中,每周平均体育运动时间超过4小时的男生人数和女生人数,列出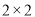 列联表,然后根据公式计算出
列联表,然后根据公式计算出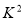 的观测值,如果
的观测值,如果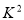 的观测值大于3.841,则就有有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”;否则就没有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的观测值大于3.841,则就有有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”;否则就没有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
试题解析:(1) 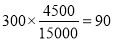 ,所以应收集90位女生的样本数据。
,所以应收集90位女生的样本数据。
(2)由频率分布直方图得1-2×(0.100+0.025)=0.75,所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75。
(3)由(2)知,300位学生中有300×0.75=225人的每周平均体育运动时间超过4小时,75人的每周平均体育运动时间不超过4小时,又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
每周平均体育运动时间与性别列联表。
| 男生 | 女生 | 总计 |
每周平均体育运动时间 不超过4小时 | 45 | 30 | 75 |
每周平均体育运动时间 超过4小时 | 165 | 60 | 225 |
总计 | 210 | 90 | 300 |
结合列联表可算得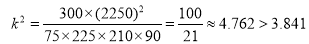 .所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
.所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
考点:1.分层抽样;2. 频率分布直方图;3.独立性检验.


科目:高中数学 来源:2015届湖南省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
设集合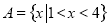 ,集合
,集合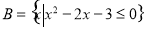 ,则
,则 ( )
( )
A、(1,4) B、(3,4)
C、(1,3) D、(1,2)∪(3,4)
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
椭圆
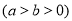 的一个焦点为
的一个焦点为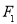 ,若椭圆上存在一个点
,若椭圆上存在一个点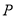 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段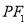 相切于该线段的中点,则椭圆的离心率为( )
相切于该线段的中点,则椭圆的离心率为( )
A. B.
B.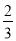 C.
C.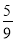 D.
D.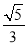
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com