
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若方程![]()
![]() 有两个相异实根
有两个相异实根![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)增区间![]() ,减区间
,减区间![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)求出导函数![]() ,在函数定义或内,通过解不等式
,在函数定义或内,通过解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)要证明题设不等式,首先要确定
得减区间;(2)要证明题设不等式,首先要确定![]() 的性质.由(1)函数的单调性知
的性质.由(1)函数的单调性知![]() ,同时由
,同时由![]() 得,
得,![]() ,从而
,从而![]() ,从要证明的结论可以看出 ,我们要证明
,从要证明的结论可以看出 ,我们要证明![]() ,由于
,由于![]() 在
在![]() 上是递增的,因此可证
上是递增的,因此可证![]() ,作差
,作差![]() ,
,![]()
![]()
![]()
![]() ,下面要证
,下面要证![]() ,设
,设![]() ,由导数求出它的最大值,只要最大值小于0,命题即证.
,由导数求出它的最大值,只要最大值小于0,命题即证.
试题解析:(1)![]() 的定义域为
的定义域为![]()
![]()
![]()
当![]() 时
时![]() 所以
所以 ![]() 在
在![]() 递增
递增
当![]() 时
时![]() 所以
所以 ![]() 在
在![]() 递减
递减
(2)由(1)可设![]() 的两个相异实根分别为
的两个相异实根分别为![]() ,
,![]() 满足
满足![]()
且![]() ,
,![]()
由题意可知![]()
又有(1)可知![]() 在
在![]() 递减
递减
故![]()
所以![]()
令![]()
![]()
![]()
令![]()
![]() ,
,
则![]() .
.
当![]() 时,
时,![]() ,
,![]() 是减函数,所以
是减函数,所以![]()
所以当![]() 时,
时,![]() ,即
,即![]()
因为![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,故
,故![]() .
.
综上所述:![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知x0,x0+![]() 是函数f(x)=cos2(wx﹣
是函数f(x)=cos2(wx﹣![]() )﹣sin2wx(ω>0)的两个相邻的零点
)﹣sin2wx(ω>0)的两个相邻的零点
(1)求![]() 的值;
的值;
(2)若对任意![]() ,都有f(x)﹣m≤0,求实数m的取值范围.
,都有f(x)﹣m≤0,求实数m的取值范围.
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的解,求实数
上有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=![]() x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣
x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣![]() ,
, ![]() ).
).
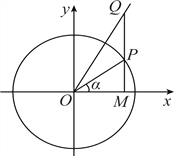
(Ⅰ)若sinα=![]() ,求cos∠POQ;
,求cos∠POQ;
(Ⅱ)求△OPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 、
、![]() ,并且直线
,并且直线![]() :
: ![]() 平分圆
平分圆![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
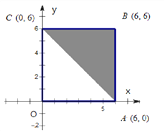
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中不正确命题的个数是( )
①过空间任意一点有且仅有一个平面与已知平面垂直
②过空间任意一条直线有且仅有一个平面与已知平面垂直
③过空间任意一点有且仅有一个平面与已知的两条异面直线平行
④过空间任意一点有且仅有一条直线与已知平面垂直
A.1 B.2
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com