
 -
- |≤|
|≤| |-|
|-| |;②
|;② ,
, 共线,
共线, ,
, 平,则
平,则 与
与 为平行向量;③
为平行向量;③ ,
, ,
, 为相互不平行向量,则(
为相互不平行向量,则(
 )
) -(
-( -
- )
) 与
与 垂直;④在△ABC中,若a2taanB=b2tanA,则△ABC一定是等腰直角三角形;⑤
垂直;④在△ABC中,若a2taanB=b2tanA,则△ABC一定是等腰直角三角形;⑤ •
• =
= •
• ,则
,则 ⊥(
⊥( -
- )
) 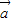 -
-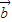 |≤|
|≤|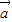 |-|
|-|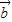 |,当向量
|,当向量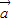 与
与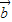 反向,且|
反向,且|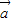 |>|
|>|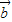 |时取等号,故①正确;
|时取等号,故①正确;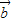 =
=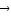 ,则当
,则当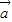 ,
,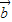 共线,
共线,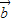 ,
,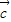 平行均成立时,则
平行均成立时,则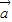 与
与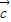 为也可能不平行,故②错误;
为也可能不平行,故②错误;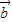
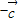 )
)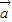 -(
-(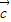 -
-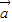 )
)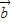 是一个数量,故③错误;
是一个数量,故③错误;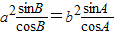 ,即
,即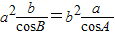
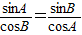 ,即sin2A=sin2B
,即sin2A=sin2B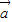 •
•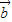 =
=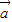 •
•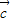 ,则
,则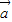 •
•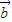 -
-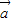 •
•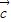 =0,即
=0,即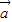 •(
•(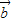 -
-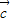 )=0,则
)=0,则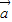 ⊥(
⊥(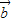 -
-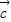 ),故⑤正确;
),故⑤正确;

科目:高中数学 来源: 题型:
| BC |
| CA |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com