
【题目】已知椭圆C: ![]() (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,M为直线x=﹣3上任意一点,过F作MF的垂线交椭圆C于点P,Q.证明:OM经过线段PQ的中点N.(其中O为坐标原点)
【答案】
(1)解:由题意可得c=2,
短轴的两个端点与长轴的一个端点构成正三角形,可得
a= ![]() 2b,即有a=
2b,即有a= ![]() b,a2﹣b2=4,
b,a2﹣b2=4,
解得a= ![]() ,b=
,b= ![]() ,
,
则椭圆方程为 ![]() =1;
=1;
(2)证明:设M(﹣3,m),P(x1,y1),Q(x2,y2),
PQ的中点为N(x0,y0),kMF=﹣m,
由F(﹣2,0),可设直线PQ的方程为x=my﹣2,
代入椭圆方程可得(m2+3)y2﹣4my﹣2=0,
即有y1+y2= ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
于是N(﹣ ![]() ,
, ![]() ),
),
则直线ON的斜率kON=﹣ ![]() ,
,
又kOM=﹣ ![]() ,
,
可得kOM=kON,
则O,N,M三点共线,即有OM经过线段PQ的中点.
【解析】(1)由椭圆C的焦距为4,及等边三角形的性质和a2=b2+c2 , 求得a,b,即可求椭圆C的标准方程;(2)设M(﹣3,m),P(x1 , y1),Q(x2 , y2),PQ的中点为N(x0 , y0),kMF=﹣m,设直线PQ的方程为x=my﹣2,代入椭圆方程,运用韦达定理和中点坐标公式,结合三点共线的方法:斜率相等,即可得证.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】2018年俄罗斯世界杯激战正酣,某校工会对全校教职工在世界杯期间每天收看比赛的时间作了一次调查,得到如下频数分布表:
收看时间 (单位:小时) |
|
|
|
|
|
|
| 14 |
|
| 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“球迷”,否则定义为“非球迷”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
球迷 | 40 | ||
非球迷 |
| ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“球迷”与“性别”有关;
(2)在全校“球迷”中按性别分层抽样抽取6名,再从这6名“球迷”中选取2名世界杯知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图. 
(1)试估计该校数学的平均成绩(同一组中的数据用该区间的中点值作代表);
(2)这50名学生中成绩在120分以上的同学中任意抽取3人,该3人在130分(含130分)以上的人数记为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求直线![]() 在矩阵
在矩阵![]() 对应变换作用下的直线
对应变换作用下的直线![]() 的方程;
的方程;
(2)在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 以原点
以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,求曲线C与直线
,求曲线C与直线![]() 交点的极坐标
交点的极坐标![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2. 
(1)求证:BE∥平面PAD;
(2)求证:BC⊥平面PBD;
(3)在线段PC上是否存在一点Q,使得二面角Q﹣BD﹣P为45°?若存在,求 ![]() 的值;若不存在,请述明理由.
的值;若不存在,请述明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,该椭圆中心到直线
,该椭圆中心到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
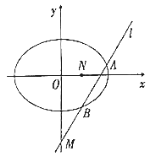
(2)是否存在过点![]() 的直线
的直线![]() ,使直线
,使直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过定点
为直径的圆过定点![]() ?若存在,求出所有符合条件的直线方程;若不存在,请说明理由.
?若存在,求出所有符合条件的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )在同一半周期内的图象过点
)在同一半周期内的图象过点![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 为坐标原点,
为坐标原点, ![]() 为函数
为函数![]() 图象的最高点,
图象的最高点, ![]() 为函数
为函数![]() 的图象与
的图象与![]() 轴的正半轴的交点,
轴的正半轴的交点, ![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求![]() 的值;
的值;
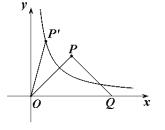
(2)将![]() 绕原点
绕原点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() ,得到
,得到![]() ,若点
,若点![]() 恰好落在曲线
恰好落在曲线![]() (
(![]() )上(如图所示),试判断点
)上(如图所示),试判断点![]() 是否也落在曲线
是否也落在曲线![]() (
(![]() )上,并说明理由.
)上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com