
【题目】已知![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 的最小值为1,此时直线
的最小值为1,此时直线![]() :
:![]()
【解析】
(1)用直接法求轨迹方程,即设动点为![]() ,把已知用坐标表示并整理即得.注意取值范围;
,把已知用坐标表示并整理即得.注意取值范围;
(2)设![]() :
:![]() ,将其与曲线
,将其与曲线![]() 的方程联立,消元并整理得
的方程联立,消元并整理得![]() ,
,
设![]() ,
,![]() ,则可得
,则可得![]() ,
,![]() ,由
,由![]() 求出
求出![]() ,
,
将直线![]() 方程
方程![]() 与
与![]() 联立,得
联立,得![]() ,求得
,求得![]() ,计算
,计算![]() ,设
,设![]() .显然
.显然![]() ,构造
,构造![]() ,由导数的知识求得其最小值,同时可得直线
,由导数的知识求得其最小值,同时可得直线![]() 的方程.
的方程.
(1)设![]() ,则
,则![]() ,即
,即![]()
整理得![]()
(2)设![]() :
:![]() ,将其与曲线
,将其与曲线![]() 的方程联立,得
的方程联立,得![]()
即![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
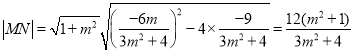
将直线![]() :
:![]() 与
与![]() 联立,得
联立,得![]()
∴![]()
∴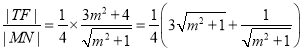
设![]() .显然
.显然![]()
构造![]()
![]() 在
在![]() 上恒成立
上恒成立
所以![]() 在
在![]() 上单调递增
上单调递增
所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取“=”
时取“=”
即![]() 的最小值为1,此时直线
的最小值为1,此时直线![]() :
:![]() .
.
(注:1.如果按函数![]() 的性质求最值可以不扣分;2.若直线方程按斜率是否存在讨论,则可以根据步骤相应给分.)
的性质求最值可以不扣分;2.若直线方程按斜率是否存在讨论,则可以根据步骤相应给分.)


科目:高中数学 来源: 题型:
【题目】某城市有东、西、南、北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵,交警部门记录了11月份30天内的拥堵情况(如下表所示,其中●表示拥堵,○表示通畅).假设每个人口是否发生拥堵相互独立,将各入口在这30天内拥堵的频率代替各入口每天拥堵的概率.
11.1 | 11.2 | 11.3 | 11.4 | 11.5 | 11.6 | 11.7 | 11.8 | 11.9 | 11.10 | 11.11 | 11.12 | 11.13 | 11.14 | 11.15 | ||||||||||||||||
东入口 | ● | ○ | ○ | ○ | ○ | ● | ○ | ● | ● | ○ | ● | ● | ● | ○ | ● | |||||||||||||||
西入口 | ○ | ○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ● | ○ | ○ | |||||||||||||||
南入口 | ○ | ● | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ● | |||||||||||||||
北入口 | ● | ○ | ○ | ○ | ● | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ● | ○ | |||||||||||||||
11.16 | 11.17 | 11.18 | 11.19 | 11.20 | 11.21 | 11.22 | 11.23 | 11.24 | 11.25 | 11.26 | 11.27 | 11.28 | 11.29 | 11.30 | ||||||||||||||||
东入口 | ● | ○ | ○ | ● | ○ | ○ | p>○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | |||||||||||||||
西入口 | ● | ○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | |||||||||||||||
南入口 | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ● | |||||||||||||||
北入口 | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ● | ○ | |||||||||||||||
(1)分别求该城市一天中早高峰时间段这四个主干道的入口发生拥堵的概率.
(2)各人口一旦出现拥堵就需要交通协管员来疏通,聘请交通协管员有以下两种方案可供选择.方案一:四个主干道入口在早高峰时间段每天各聘请一位交通协管员,聘请每位交通协管员的日费用为![]() (
(![]() ,且
,且![]() )元.方案二:在早高峰时间段若某主干道入口发生拥堵,交警部门则需临时调派两位交通协管员协助疏通交通,调派后当日需给每位交通协管员的费用为200元.以四个主干道入口聘请交通协管员的日总费用的数学期望为依据,你认为在这两个方案中应该如何选择?请说明理由.
)元.方案二:在早高峰时间段若某主干道入口发生拥堵,交警部门则需临时调派两位交通协管员协助疏通交通,调派后当日需给每位交通协管员的费用为200元.以四个主干道入口聘请交通协管员的日总费用的数学期望为依据,你认为在这两个方案中应该如何选择?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家每年都会对中小学生进行体质健康监测,一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计,发现一分钟跳绳个数最低为10,最高为189.现将跳绳个数分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6组,并绘制出如下的频率分布直方图.
6组,并绘制出如下的频率分布直方图.
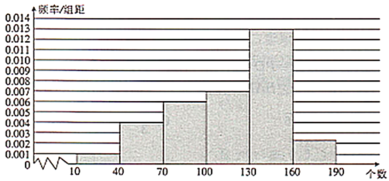
(1)若一分钟跳绳个数达到160为优秀,求该校六年级学生一分钟跳绳为优秀的人数;
(2)上级部门要对该校体质监测情况进行复查,发现每组男、女学生人数比例有很大差别,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() .试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
.试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,其中m是不等于零的常数.
,其中m是不等于零的常数.
(1)![]() 时,直接写出
时,直接写出![]() 的值域;
的值域;
(2)求![]() 的单调递增区间;
的单调递增区间;
(3)已知函数![]() ,
,![]() ,定义:
,定义:![]() ,
,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() 表示函数
表示函数![]() 在
在![]() 上的最小值,
上的最小值,![]() 表示函数
表示函数![]() 在
在![]() 上的最大值.例如:
上的最大值.例如:![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .当
.当![]() 时,
时,![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),与数列
),与数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),记
),记![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的表达式;
的表达式;
(3)已知![]() ,且存在正整数
,且存在正整数![]() ,使得在
,使得在![]() 中有4项为100,求
中有4项为100,求![]() 的值,并指出哪4项为100.
的值,并指出哪4项为100.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com