
【题目】在平面直角坐标系xoy中,曲线C的参数方程是![]() (θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:
(θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:![]()
(1)求曲线C的极坐标方程;
(2)设直线θ=![]() 与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】下列4个命题:
(1)有两个面互相平行,其余四个面都是全等的等腰梯形的六面体是正四棱台;
(2)底面是正三角形,其余各面都是等腰三角形的棱锥是正三棱锥;
(3)各侧面都是等腰三角形的四棱锥是正四棱锥;
(4)底面是正三角形,相邻两侧而所成的二面角都相等的三棱锥是正三棱锥
中,假命题的个数为( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆C:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,直线l:
,直线l:![]() 与椭圆C交于A,B两点
与椭圆C交于A,B两点![]() 为坐标原点.
为坐标原点.
![]() 若直线l过点
若直线l过点![]() ,且
,且![]() 十
十![]() ,求直线l的方程;
,求直线l的方程;
![]() 若以AB为直径的圆过点O,点P是线段AB上的点,满足
若以AB为直径的圆过点O,点P是线段AB上的点,满足![]() ,求点P的轨迹方程.
,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.
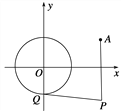
(1)求a,b间的关系;
(2)求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位
平均增加5个单位
③线性回归方程![]() 必过
必过![]()
④设具有相关关系的两个变量![]() 的相关系数为
的相关系数为![]() ,那么
,那么![]() 越接近于0,
越接近于0,![]() 之间的线性相关程度越高;
之间的线性相关程度越高;
⑤在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,那么
的值,那么![]() 的值越大,判断两个变量间有关联的把握就越大。
的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com