
分析 由题意,∠ADC=150°,则,∠ADB=30°,∠B=30°,可得AB=AD.利用余弦定理可得AB的长度.根据△ABC的面积S=$\frac{1}{2}$AB•BC•sinB可得答案.
解答 解:由题意D在边BC上,∠ADC=150°,
∴,∠ADB=30°,∠B=30°,
∴AB=AD.
余弦定理可得:cos30°=$\frac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2AB•BD}$,BD=2,
可得:AB=AD=$\frac{2\sqrt{3}}{3}$
DC=1,则BC=3
△ABC的面积S=$\frac{1}{2}$AB•BC•sinB=$\frac{1}{2}×\frac{2\sqrt{3}}{3}×3×\frac{1}{2}$=$\frac{\sqrt{3}}{2}$
故答案为:$\frac{2\sqrt{3}}{3}$,$\frac{\sqrt{3}}{2}$
点评 本题考查三角形的余弦定理的运用,考查运算能力,属于基础题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:解答题
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5;4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(I)求取出的3个球编号都不相同的概率;
(II)记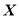 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求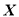 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com