
已知函数 ,且
,且 .
.
(1)求 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)设函数 ,若函数
,若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科运用导数法确定函数的极值、最值、图像(解析版) 题型:选择题
设动直线 与函数
与函数 的图象分别交于点M、N,则|MN|的最小值为( )
的图象分别交于点M、N,则|MN|的最小值为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题后三题(解析版) 题型:解答题
已知函数
(1)当 时,求函数
时,求函数 的单调区间和极值。
的单调区间和极值。
(2)若函数 在[1,4]上是减函数,求实数
在[1,4]上是减函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题后三题(解析版) 题型:解答题
设函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)求函数 的单调区间;
的单调区间;
(2)记曲线 在点
在点 (其中
(其中 )处的切线为
)处的切线为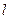 ,
,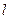 与
与 轴、
轴、 轴所围成的三角形面积为
轴所围成的三角形面积为 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科绝对值不等式(解析版) 题型:选择题
已知不等式|2x-t|+t-1<0的解集为 ,则t=( )
,则t=( )
A. 0
B. -1
C. -2
D. -3
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科空间垂直、平行关系(解析版) 题型:选择题
在正方体 中,M是棱
中,M是棱 的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com