
设函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)求函数 的单调区间;
的单调区间;
(2)记曲线 在点
在点 (其中
(其中 )处的切线为
)处的切线为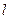 ,
,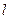 与
与 轴、
轴、 轴所围成的三角形面积为
轴所围成的三角形面积为 ,求
,求 的最大值.
的最大值.
 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2014高考名师推荐数学文科选择题专项训练(解析版) 题型:选择题
数列 是公差不为0的等差数列,且
是公差不为0的等差数列,且 为等比数列
为等比数列 的连续三项,则数列
的连续三项,则数列 的公比为( )
的公比为( )
A. B.4 C.2 D.
B.4 C.2 D.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科证明不等式(解析版) 题型:选择题
已知a,b为非零实数,则使不等式: 成立的一个充分而不必要条件是( )
成立的一个充分而不必要条件是( )
A. ab>0
B. ab<0
C. a>0,b<0
D. a>0,b>0
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题后三题(解析版) 题型:解答题
已知函数 ,且
,且 .
.
(1)求 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)设函数 ,若函数
,若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题前三题(解析版) 题型:解答题
设等差数列{an}的首项a1为a,公差d=2,前n项和为Sn.
(1) 若当n=10时,Sn取到最小值,求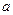 的取值范围;
的取值范围;
(2) 证明: n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科相互独立事件(解析版) 题型:选择题
甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜,根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是( )
A.0.216 B.0.36 C.0.432 D.0.648
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com