练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设．

    （1）若曲线在点处的切线方程为，求的值；

    （2）当时，求的单调区间与极值．

     

    （1），

    （2）单调增区间是，减区间是，极小值

    求导可得．

    【解析】（1）由，，解得，．

    （2）函数的定义域是．

    当时，，．

    令，求导可得．

    当时，，则，是减函数；

    当时，，则，是增函数．

    故的单调增区间是，减区间是，当时，有极小值．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科余弦定理（解析版） 题型：选择题

    △ABC的三内角A，B，C所对边长分别是a，b，c，设向量m＝(a＋b，sinC)，n＝(a＋c，sinB－sinA)，若m∥n，则角B的大小为（    ）

    A．30°

    B．60°

    C．120°

    D．150°

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科三角函数图象变换（解析版） 题型：选择题

    把函数y＝cos2x＋1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

    已知函数，的最大值为3，的图像的相邻两对称轴间的距离为2，在轴上的截距为2．

    （1）求函数的解析式；

    （2）求的单调递增区间．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

    如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.

    （1）求证：CE⊥平面PAD；

    （2）若PA=AB=1，AD=3，CD=，∠CDA=45°，求四棱锥P-ABCD的体积.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

    某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，其可见部分如下，据此解答如下问题：

     

    （1）计算频率分布直方图中[80,90)间的矩形的高；

    （2）若要从分数在之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份试卷的分数在之间的概率；

    （3）根据频率分布直方图估计这次测试的平均成绩．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

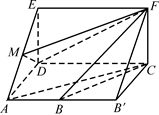
    如图，四边形ABCD是梯形，四边形CDEF是矩形，且平面ABCD⊥平面CDEF，∠BAD＝∠CDA＝90°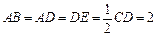，，M是线段AE上的动点．

    （1）试确定点M的位置，使AC∥平面MDF，并说明理由；

    （2）在（1）的条件下，求平面MDF将几何体ADE－BCF分成的两部分的体积之比．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科选择题专项训练（解析版） 题型：选择题

    一空间几何体的三视图如图所示，该几何体的体积为12π＋，则正视图中

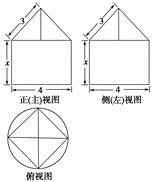
    x的值为(    )

    A.5 B.4 C.3 D.2

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解答题后三题（解析版） 题型：解答题

    设函数，其中为自然对数的底数.

    （1）求函数的单调区间；

    （2）记曲线在点（其中）处的切线为，与轴、轴所围成的三角形面积为，求的最大值.

     

    查看答案和解析>>

    同步练习册答案