
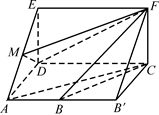
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,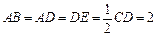 ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014高考名师推荐数学理科二项式定理与性质(解析版) 题型:选择题
设m为正整数, 展开式的二项式系数的最大值为
展开式的二项式系数的最大值为 展开式的二项式系数的最大值为b.若
展开式的二项式系数的最大值为b.若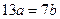 ,则m=( )
,则m=( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科频率分布直方图、茎叶图(解析版) 题型:选择题
在样本的频率分布直方图中,共有n个小矩形,若中间一个小矩形的面积等于其余(n-1)个小矩形面积的 ,且样本容量为300,则中间一组的频数为( )
,且样本容量为300,则中间一组的频数为( )
A.30 B.40 C.50 D.60
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
已知实数 ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数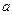 的值;
的值;
(2)若等差数列 的首项和公差都为
的首项和公差都为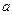 ,等比数列
,等比数列 的首项和公比都为
的首项和公比都为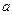 ,数列
,数列 和
和 的前
的前 项和分别为
项和分别为 ,且
,且 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科集合的表示、集合的运算、集合间的运算关系(解析版) 题型:选择题
设集合 ,则集合
,则集合 等于
等于
A. ( ,-1)
,-1)
B. (-l,1)
C. 
D. (1,+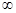 )
)
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科选择题专项训练(解析版) 题型:选择题
设复数z满足iz=2-i(i为虚数单位),则z=( )
A.-1-2i B.1-2i
C.1+2i D.-1+2i
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科选择题专项训练(解析版) 题型:选择题
数列 是公差不为0的等差数列,且
是公差不为0的等差数列,且 为等比数列
为等比数列 的连续三项,则数列
的连续三项,则数列 的公比为( )
的公比为( )
A. B.4 C.2 D.
B.4 C.2 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com