
已知函数f(x)=cos(2x+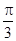 )+sin2x
)+sin2x
(1)求函数f(x)的单调递减区间及最小正周期;
(2)设锐角△ABC的三内角A,B,C的对边分别是a,b,c,若c=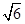 ,cosB=
,cosB=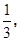
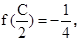 求b.
求b.
(1)最小正周期T=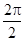 =π,f(x)的单调递减区间是[kπ-
=π,f(x)的单调递减区间是[kπ-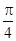 ,kπ+
,kπ+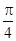 ](k∈Z).
](k∈Z).
(2) b=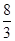 .
.
【解析】
试题分析:(1)∵f(x)=cos(2x+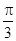 )+sin2x=cos2xcos
)+sin2x=cos2xcos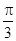 -sin2xsin
-sin2xsin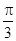 +
+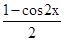
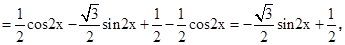
∴最小正周期T=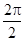 =π,令2kπ-
=π,令2kπ-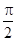 ≤2x≤2kπ+
≤2x≤2kπ+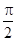 (k∈Z),得kπ-
(k∈Z),得kπ-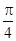 ≤x≤kπ+
≤x≤kπ+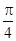 ,k∈Z,
,k∈Z,
∴f(x)的单调递减区间是[kπ-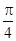 ,kπ+
,kπ+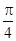 ](k∈Z).
](k∈Z).
(2)由(1)得f(x)=-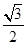 sin2x+
sin2x+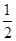 ,
,
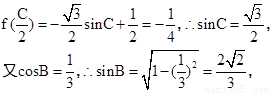
∴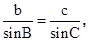 即
即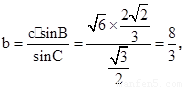 故b=
故b=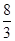 .
.
考点:本题主要考查三角函数的和差倍半公式,正弦定理的应用,三角函数的图象和性质。
点评:中档题,近些年,涉及三角函数、三角形的题目常常出现在高考题中,往往需要综合应用三角公式化简函数,以进一步研究函数的性质。应用正弦定理、余弦定理求边长、角等,有时运用函数方程思想,问题的解决较为方便。


科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| m |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com