
【题目】如图,在口![]() 中,
中, ![]() ,沿
,沿![]() 将
将![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.
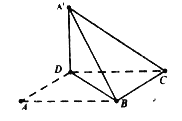
(1)求证: ![]() 平面
平面![]() ;
;
(2)若在线段![]() 上有一点
上有一点![]() 满足
满足![]() ,且二面角
,且二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为![]() (
(![]() 为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=
为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=![]() 时,这两个交点重合.
时,这两个交点重合.
(1) 求曲线C1,C2的直角坐标方程
(2) 设当 α=![]() 时,l与C1,C2的交点分别为A1,B1,当 α=-
时,l与C1,C2的交点分别为A1,B1,当 α=-![]() 时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中国决胜全面建成小康社会的关键之年,如何更好地保障和改善民生,如何切实增强政策“获得感”,成为![]() 年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊
年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊![]() 个民生项目,得到如下信息:①若该地区引进甲项目,就必须引进与之配套的乙项目;②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;③乙、丙两个项目之间有冲突,两个项目只能引进一个;④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;⑤若引进项目戊,甲、丁两个项目也必须引进.则该地区应引进的项目为( )
个民生项目,得到如下信息:①若该地区引进甲项目,就必须引进与之配套的乙项目;②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;③乙、丙两个项目之间有冲突,两个项目只能引进一个;④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;⑤若引进项目戊,甲、丁两个项目也必须引进.则该地区应引进的项目为( )
A. 甲、乙B. 丙、丁C. 乙、丁D. 甲、丙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率,(单位:![]() )与管道半径r(单位:cm)的四次方成正比.
)与管道半径r(单位:cm)的四次方成正比.
(1)写出气体流量速率,关于管道半径r的函数解析式;
(2)若气体在半径为3cm的管道中,流量速率为![]() ,求该气体通过半径为r的管道时,其流量速率v的表达式;
,求该气体通过半径为r的管道时,其流量速率v的表达式;
(3)已知(2)中的气体通过的管道半径为5cm,计算该气体的流量速率(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图(1)是某条公共汽车线路收支差额y关于乘客量x的图象.



(1)试说明图(1)上点A,点B以及射线AB上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图(2)(3)所示,你能根据图象,说明这两种建议是什么吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :关于
:关于![]() 的不等式
的不等式![]() 无解;命题
无解;命题![]() :指数函数
:指数函数![]() 是
是![]() 上的增函数.
上的增函数.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若满足![]() 为假命题且
为假命题且![]() 为真命题的实数
为真命题的实数![]() 取值范围是集合
取值范围是集合![]() ,集合
,集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com