练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】图（1）是某条公共汽车线路收支差额y关于乘客量x的图象.

    （1）试说明图（1）上点A，点B以及射线AB上的点的实际意义；

    （2）由于目前本条线路亏损，公司有关人员提出了两种扭亏为赢的建议，如图（2）（3）所示，你能根据图象，说明这两种建议是什么吗？

    【答案】（1）点A见解析，点B见解析，射线AB见解析；（2）两种建议见解析

    【解析】

    （1）观察函数图象可知，函数的横坐标表示乘客量，纵坐标表示收支差额，即可得出结论．

    （2）观察函数图象可知，函数的横坐标表示乘客量，纵坐标表示收支差额，根据图象，即可得出合理的建立．

    解：（1）点A的实际意义为：当乘客量为0时，公司亏损1（单位）；点B的实际意义为：当乘客量为1.5时，公司收支持平；

    射线AB上的点的实际意义为：当乘客量小于1.5时，公司将亏损；当乘客量大于1.5时，公司将赢利.

    （2）题图（2）的建议是：降低成本而保持票价不变；题图（3）的建议是：提高票价而保持成本不变.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了调查某大学学生在某天上网的时间，随机对100名男生和100名女生进行了不记名的问卷调查，得到了如下的统计结果：

    (1)若该大学共有女生750人，试估计其中上网时间不少于60分钟的人数；

    (2)完成联表，并回答能否有90%的把握认为“大学生上网时间与性别有关”.

    附：，其中n＝a＋b＋c＋d为样本容量.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为定义域R上的奇函数，且在R上是单调递增函数，函数，数列为等差数列，且公差不为0，若，则( )

    A. 45B. 15C. 10D. 0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在口中， ，沿将翻折到的位置，使平面平面.

    （1）求证： 平面；

    （2）若在线段上有一点满足，且二面角的大小为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【选修4-4，坐标系与参数方程】

    在直角坐标系中，直线的参数方程为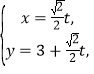（t为参数），在以O为极点，轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为

    （Ⅰ）求直线的普通方程与曲线C的直角坐标方程；

    （Ⅱ）若直线与轴的交点为P，直线与曲线C的交点为A,B,求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是圆O的直径，点C是圆O上异于A，B的点，直线平面，E，F分别是，的中点.

    （1）记平面与平面的交线为l，试判断直线l与平面的位置关系，并加以证明；

    （2）设，求二面角大小的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中，错误的是（ ）

    A. 若命题，，则命题，

    B. “”是“”的必要不充分条件

    C. “若，则、中至少有一个不小于”的逆否命题是真命题

    D. ，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：关于x的方程x2﹣ax+4=0有实根；命题q：关于x的函数y=2x2+ax+4在[3，+∞）上是增函数，若“p或q”是真命题，“p且q”是假命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设的内角所对的边为,则下列命题正确的是_____．

    ①若，则； ②若，则；

    ③若，则； ④若，则．

    查看答案和解析>>

    同步练习册答案