
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源:不详 题型:解答题
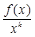 在
在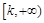 上为增函数,则称
上为增函数,则称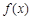 为“k次比增函数”,其中
为“k次比增函数”,其中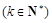 . 已知
. 已知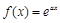 其中e为自然对数的底数.
其中e为自然对数的底数.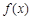 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;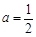 时,求函数
时,求函数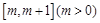 在
在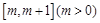 上的最小值;
上的最小值;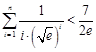 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
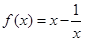 .
.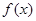 的奇偶性,并加以证明;
的奇偶性,并加以证明;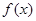 在区间
在区间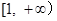 上为增函数;
上为增函数;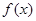 在区间
在区间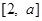 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于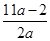 ,求
,求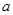 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
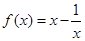 ,
, .
.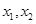 ,其中
,其中 ,求
,求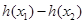 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(3,7) | B.(9,25) | C.(13,49) | D.(9, 49) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
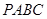 沿
沿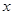 轴滚动,点
轴滚动,点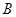 恰好经过原点.设顶点
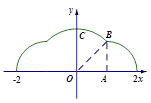
恰好经过原点.设顶点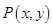 的轨迹方程是
的轨迹方程是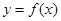 ,则对函数
,则对函数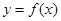 有下列判断:①函数
有下列判断:①函数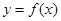 是偶函数;②对任意的
是偶函数;②对任意的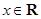 ,都有
,都有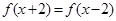 ;③函数
;③函数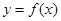 在区间
在区间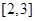 上单调递减;④函数
上单调递减;④函数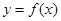 在区间
在区间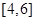 上是减函数.其中判断正确的序号是 .
上是减函数.其中判断正确的序号是 .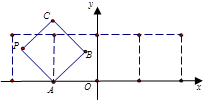
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com