
分析 根据题意,利用△ABC的面积求出|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|的值,再利用$\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$求出D是BC的四等分点,计算S△ABD和S△ACD的值,求|$\overrightarrow{AB}$|•|$\overrightarrow{DE}$|•|$\overrightarrow{AC}$|•|$\overrightarrow{DF}$|的值,从而求出|$\overrightarrow{DE}$|•|$\overrightarrow{DF}$|的值,计算数量积$\overrightarrow{DE}$•$\overrightarrow{DF}$的值.
解答 解:如图所示,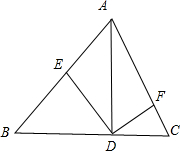
△ABC中,cosA=$\frac{3}{5}$,∴sinA=$\sqrt{1{-cos}^{2}A}$=$\frac{4}{5}$;
∴S△ABC=$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|sinA=$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•$\frac{4}{5}$=8,
即|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=20;
设$\overrightarrow{BD}$=λ$\overrightarrow{BC}$,λ∈(0,1),
则$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+λ($\overrightarrow{AC}$-$\overrightarrow{AB}$)=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AC}$,
又$\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,∴λ=$\frac{3}{4}$;
∴$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{\frac{1}{2}BD•h}{\frac{1}{2}CD•h}$=$\frac{BD}{CD}$=$\frac{3}{1}$=3,
∴S△ABD=$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{DE}$|=$\frac{3}{4}$×8=6,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{DE}$|=12;
又S△ACD=$\frac{1}{2}$|$\overrightarrow{AC}$|•|$\overrightarrow{DF}$|=2,
∴|$\overrightarrow{AC}$|•|$\overrightarrow{DF}$|=4;
∴|$\overrightarrow{AB}$|•|$\overrightarrow{DE}$|•|$\overrightarrow{AC}$|•|$\overrightarrow{DF}$|=48,
∴|$\overrightarrow{DE}$|•|$\overrightarrow{DF}$|=$\frac{48}{20}$=$\frac{12}{5}$,
∴$\overrightarrow{DE}$•$\overrightarrow{DF}$=|$\overrightarrow{DE}$|•|$\overrightarrow{DF}$|•cos(180°-A)=$\frac{12}{5}$×(-$\frac{3}{5}$)=-$\frac{36}{25}$.
故答案为:-$\frac{36}{25}$.
点评 本题考查了平面向量的数量积与三角形面积公式的应用问题,是综合题.


科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 合计 | |
| 男同学 | 24 | 6 | 30 |
| 女同学 | 6 | 14 | 20 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,4,5} | B. | {2,4,5} | C. | {1,2,5} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3e-4,1) | B. | [-3e-4,1)∪{-e-2} | C. | [0,1)∪{-e-2} | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ-$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z | ||
| C. | [kπ-$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ+$\frac{5π}{12}$,kπ-$\frac{11π}{12}$],k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,e) | B. | (-∞,e) | C. | {e} | D. | (-∞,0)∪{e} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com