
分析 根据函数与方程之间的关系转化为两个图象的交点问题,利用数形结合进行求解即可.
解答 解:可以将问题转化为研究函数函数$g(x)=sin(ωx+\frac{π}{6})$(ω>0)与直线$y=\frac{1}{2}$有且仅有5个交点.如图,是满足条件的两个临界状态,由此得到$ω\frac{π}{4}+\frac{π}{6}=4π+\frac{π}{6}$,$ω\frac{π}{4}+\frac{π}{6}=4π+\frac{5π}{6}$,计算可得临界态的$ω=16,ω=\frac{56}{3}$,依据题意可得$ω∈[16,\frac{56}{3})$.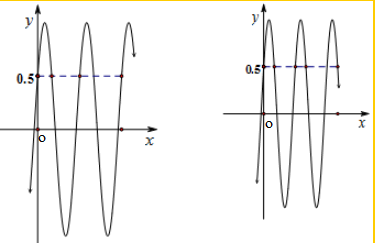
故答案为:$[16,\frac{56}{3})$
点评 本题主要考查函数与方程零点的应用,利用数形结合转化为两个函数的交点个数问题是解决本题的关键.综合性较强,有一定的难度.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | 若($\sqrt{x}$-$\frac{1}{2\root{3}{x}}$)n的展开式中第四项为常数项,则n=5 | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a1+a2>0,则a1+a3>0 | B. | 若a1+a3>0,则a1+a2>0 | ||
| C. | 若a1>0,则S2017>0 | D. | 若a1>0,则S2016>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
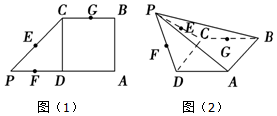 在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD如图(2).
在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD如图(2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com