
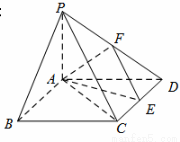
如图,在四棱锥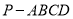 中,底面
中,底面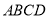 是矩形,
是矩形,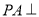 平面
平面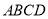 ,
,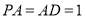 ,
, ,点
,点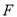 是
是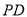 的中点,点
的中点,点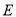 是边
是边 上的任意一点.
上的任意一点.
(Ⅰ)当点 为
为 边的中点时,判断
边的中点时,判断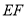 与平面
与平面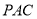 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)证明:无论点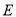 在
在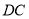 边的何处,都有
边的何处,都有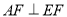 ;
;
(Ⅲ)求三棱锥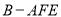 的体积.
的体积.
科目:高中数学 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市毕业生二月调研测试理科数学试卷(解析版) 题型:选择题
已知点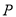 为曲线
为曲线 上任意一点,O为坐标原点,则
上任意一点,O为坐标原点,则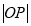 的最小值为
的最小值为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省等高三上学期三校联考理科数学试卷(解析版) 题型:填空题
正偶数列有一个有趣的现象:① ;②
;②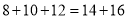 ;
;
③
按照这样的规律,则2012在第 个等式中。
查看答案和解析>>
科目:高中数学 来源:2015年东北三省四市教研联合体高考模拟试卷(一)理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数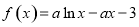 (
( ).
).
(1)讨论 的单调性;
的单调性;
(2)若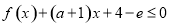 对任意
对任意 恒成立,求实数
恒成立,求实数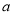 的取值范围(
的取值范围(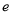 为自然常数);
为自然常数);
(3)求证
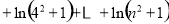

 (
( ,
, ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com