
在 中,角
中,角 、
、 、
、 所对应的边为
所对应的边为 、
、 、
、 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 ,且
,且 的面积
的面积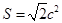 ,求
,求 的值.
的值.
(1)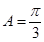 ;(2)
;(2)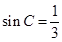 .
.
解析试题分析:(1)在等式 中利用差角公式化简求出
中利用差角公式化简求出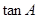 的值,从而求出角
的值,从而求出角 的值;(2)解法1是先求出
的值;(2)解法1是先求出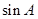 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,最后利用正弦定理求出
的等量关系,最后利用正弦定理求出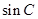 的值;解法2是是先求出
的值;解法2是是先求出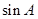 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,通过观察三者之间的等量关系发现
的等量关系,通过观察三者之间的等量关系发现 、
、 、
、 三者满足勾股定理,最后在直角三角形中求出
三者满足勾股定理,最后在直角三角形中求出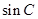 的值;解法3是先求出
的值;解法3是先求出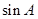 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,再利用余弦定理最终得到
之间的等量关系,再利用余弦定理最终得到 与
与 的等量关系,最后利用三角形的面积公式求出
的等量关系,最后利用三角形的面积公式求出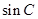 的值;解法4是先求出
的值;解法4是先求出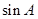 的值,借助三角形的面积公式得出
的值,借助三角形的面积公式得出 与
与 之间的等量关系,从而得出
之间的等量关系,从而得出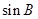 与
与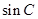 的等量关系,并利用
的等量关系,并利用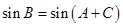 得出
得出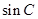 和
和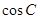 的值,最后利用
的值,最后利用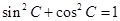 求出
求出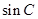 的值.
的值.
试题解析:(1)由 ,得
,得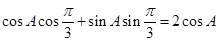 ,
,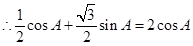 ,
,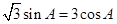 ,
, ,
,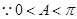 ,
,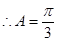 ;
;
(2)解法1: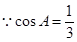 ,
,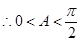 ,
,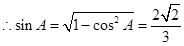 ,
,
由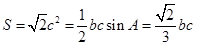 ,得
,得 ,
,
由余弦定理得: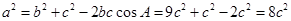 ,
,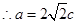 ,
,
由正弦定理得: ,即
,即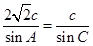 ,
,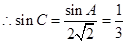 .
.
解法2: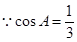 ,
,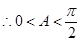 ,
,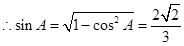 ,
,
由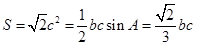 得
得 ,
,
由余弦定理得: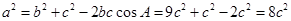 ,
,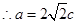 ,
,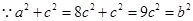 ,
,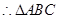 是直角三角形,角
是直角三角形,角 为直角,
为直角,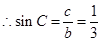 ;
;
解法3: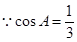 ,
,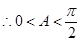 ,
,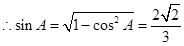 ,
,
由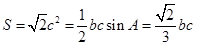 得
得
由余弦定理得: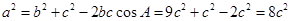 ,
,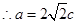 ,
,
又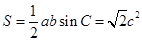 ,得
,得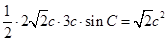 ,
,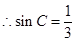 ;
;
解法4: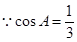 ,
,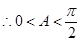 ,
,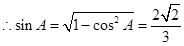 ,
,
由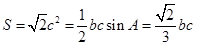 得
得


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
已知a,b,c分别为 ABC的三个内角A,B,C的对边,
ABC的三个内角A,B,C的对边, =(sinA,1),
=(sinA,1), =(cosA,
=(cosA, ),且
),且 //
// .
.
(I)求角A的大小;
(II)若a=2,b=2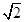 ,求
,求 ABC的面积.
ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的周期为
的周期为 ,其中
,其中 .
.
(Ⅰ)求 的值及函数
的值及函数 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,设内角A、B、C所对边的长分别为a、b、c,若
中,设内角A、B、C所对边的长分别为a、b、c,若 ,
, ,f(A)=
,f(A)= ,求b的值.
,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com