
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 4 |
分析 确定抛物线的焦点坐标,从而得到抛物线的方程和准线方程,进而可求得K的坐标,设A(x0,y0),过A点向准线作垂线AB,则B(-3,y0),根据|AK|=$\sqrt{2}$|AF|,及AF=AB=x0-(-3)=x0+3,进而可求得A点坐标.
解答 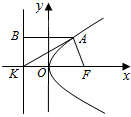 解:∵抛物线C:y2=12x,准线为x=-3,
解:∵抛物线C:y2=12x,准线为x=-3,
∴K(-3,0)
设A(x0,y0),过A点向准线作垂线AB,则B(-3,y0)
∵|AK|=$\sqrt{2}$|AF|,AF=AB=x0-(-3)=x0+3,
∴由BK2=AK2-AB2得BK2=AB2,从而y02=(x0+3)2,即12x0=(x0+3)2,
解得x0=3.
故选C.
点评 本题主要考查了抛物线的简单性质.考查了学生对抛物线基础知识的熟练掌握.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com