
分析 根据题意,画出图形,结合图形化简$\overrightarrow{BP}$,得出$\overrightarrow{OP}$=cos2θ•$\overrightarrow{OA}$,O为BC的中点,P在线段OA上,再设|$\overrightarrow{PO}$|=t,t∈[0,$\sqrt{3}$],计算($\overrightarrow{PB}$+$\overrightarrow{PC}$)•$\overrightarrow{PA}$的最大最小值即可.
解答 解:如图所示,
△ABC中,设BC的中点为O,则$\overrightarrow{BC}$=2$\overrightarrow{BO}$,
∵$\overrightarrow{BP}$=$\frac{1}{2}$sin2θ•$\overrightarrow{BC}$+cos2θ•$\overrightarrow{BA}$=sin2θ•$\overrightarrow{BO}$+cos2θ•$\overrightarrow{BA}$
=(1-cos2θ)•$\overrightarrow{BO}$+cos2θ•$\overrightarrow{BA}$
=$\overrightarrow{BO}$+cos2θ•($\overrightarrow{BA}$-$\overrightarrow{BO}$),
即$\overrightarrow{BP}$-$\overrightarrow{BO}$=cos2θ•($\overrightarrow{BA}$-$\overrightarrow{BO}$),
可得$\overrightarrow{OP}$=cos2θ•$\overrightarrow{OA}$,
又∵cos2θ∈[0,1],∴P在线段OA上,
由于BC边上的中线OA=2×sin60°=$\sqrt{3}$,
因此($\overrightarrow{PB}$+$\overrightarrow{PC}$)•$\overrightarrow{PA}$=2$\overrightarrow{PO}$•$\overrightarrow{PA}$,
设|$\overrightarrow{PO}$|=t,t∈[0,$\sqrt{3}$],
可得($\overrightarrow{PB}$+$\overrightarrow{PC}$)•$\overrightarrow{PA}$=-2t($\sqrt{3}$-t)=2t2-2$\sqrt{3}$t=2(t-$\frac{\sqrt{3}}{2}$)2-$\frac{3}{2}$,
∴当t=$\frac{\sqrt{3}}{2}$时,($\overrightarrow{PB}$+$\overrightarrow{PC}$)•$\overrightarrow{PA}$取得最小值为-$\frac{3}{2}$;
当t=0或$\sqrt{3}$时,($\overrightarrow{PB}$+$\overrightarrow{PC}$)•$\overrightarrow{PA}$取得最大值为0;
∴$(\overrightarrow{PB}+\overrightarrow{PC})•\overrightarrow{PA}$的取值范围是[-$\frac{3}{2}$,0].
故答案为:[-$\frac{3}{2}$,0].
点评 本题着重考查了向量的数量积公式及其运算性质、三角函数的图象与性质和二次函数的性质等知识,属于综合性题目.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a<c<b | C. | c>b>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
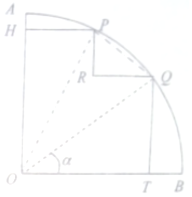 现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m<\frac{1}{4}$ | B. | m≤-2 | C. | $-2≤m<\frac{1}{4}$ | D. | m>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com