
【题目】已知直线方程为![]() ,其中
,其中![]() .
.
(1)求证:直线恒过定点;
(2)当![]() 变化时,求点
变化时,求点![]() 到直线的距离的最大值及此时的直线方程;
到直线的距离的最大值及此时的直线方程;
(3)若直线分别与![]() 轴
轴![]() 轴的负半轴交于
轴的负半轴交于![]() 两点,求
两点,求![]() 面积的最小值及此时的直线方程.
面积的最小值及此时的直线方程.
【答案】(1)证明见解析.(2)距离的最大值:![]() ,直线方程:
,直线方程:![]() (3)面积的最小值为
(3)面积的最小值为![]() ,直线的方程为
,直线的方程为![]() .
.
【解析】
(1)直线![]() 的方程化为:
的方程化为:![]() ,令
,令![]() ,解出即可得出直线
,解出即可得出直线![]() 经过定点.
经过定点.
(2)设定点为![]() ,当
,当![]() 变化时,
变化时,![]() 直线
直线![]() 时,点
时,点![]() 到直线
到直线![]() 的距离的最大,此时直线
的距离的最大,此时直线![]() 与
与![]() 垂直,可求直线方程.
垂直,可求直线方程.
(3)直线![]() 的斜率
的斜率![]() 存在且
存在且![]() ,因此可设直线
,因此可设直线![]() 的方程为
的方程为![]() ,求出直线在
,求出直线在![]() 轴、
轴、![]() 轴的截距.可得
轴的截距.可得![]() 的面积,利用基本不等式的性质即可得出结果.
的面积,利用基本不等式的性质即可得出结果.
(1)直线方程为![]() ,
,
可化为![]() 对任意
对任意![]() 都成立,
都成立,
所以![]() ,解得
,解得![]() ,
,
所以直线恒过定点![]() .
.
(2)设定点为![]()
当![]() 变化时,
变化时,![]() 直线
直线![]() 时,
时,
点![]() 到直线的距离最大,可知点
到直线的距离最大,可知点![]() 与定点
与定点![]() 的连线的距离就是所求最大值,
的连线的距离就是所求最大值,
即![]() ,
,
此时直线![]() 过点
过点![]() 且与
且与![]() 垂直,
垂直,
∴![]() ,解得
,解得![]()
故直线![]() 的方程为
的方程为![]() .
.
(3)由于直线![]() 经过定点
经过定点![]() .直线
.直线![]() 的斜率
的斜率![]() 存在且
存在且![]() ,
,
因此可设直线方程为![]()
可得与![]() 轴、
轴、![]() 轴的负半轴交于
轴的负半轴交于![]() ,
,![]() 两点
两点
∴![]() ,
,![]() ,解得
,解得![]() .
.
∴![]()
当且仅当![]() 时取等号,面积的最小值为4
时取等号,面积的最小值为4
此时直线![]() 的方程为:
的方程为:![]() ,化为:
,化为:![]() .
.


科目:高中数学 来源: 题型:
【题目】我国华南沿海地区是台风登陆频繁的地区,为统计地形地貌对台风的不同影响,把华南沿海分成东西两区,对台风的强度按风速划分为:风速不小于30米/秒的称为强台风,风速小于30米/秒的称为风暴,下表是2014年对登陆华南地区的15次台风在东西两部的强度统计:

(1)根据上表,计算有没有99%以上的把握认为台风强度与东西地域有关;
(2)2017年8月23日,“天鸽”在深圳登陆,造成深圳特大风暴,如图所示的茎叶图统计了深圳15块区域的风速.(十位数为茎,个位数为叶)
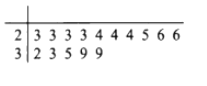
①任取2个区域进行统计,求取到2个区域风速不都小于25的概率;
②任取3个区域进行统计, ![]() 表示“风速达到强台风级别的区域个数”,求
表示“风速达到强台风级别的区域个数”,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: 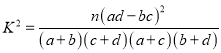 ,其中
,其中![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 的底面ABCD是边长为a的菱形,
的底面ABCD是边长为a的菱形,![]() 面ABCD,
面ABCD,![]() ,E,F分别是CD,PC的中点.
,E,F分别是CD,PC的中点.

(1)求证:平面![]() 平面PAB;
平面PAB;
(2)M是PB上的动点,EM与平面PAB所成的最大角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xln x,g(x)=x3+ax2-x+2.
(1)如果函数g(x)在区间![]() 上单调递减,求实数a的取值范围;
上单调递减,求实数a的取值范围;
(2)对任意x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
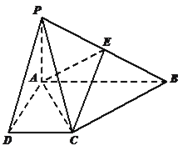
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)若棱![]() 上存在一点
上存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com